Konstruerbare tall

Konstruerbare tall tall er definert å være lengder av linjestykker i det euklidske planet som lar seg konstruere kun ved bruk av passer og linjal. De vil derfor kunne kombineres ved de fire aritmetiske regneoperasjonene addisjon, subtraksjon, multiplikasjon og divisjon samt ha en konstruerbar kvadratrot. Kubikkrøtter og høyre røtter lar seg ikke beregne ved slike konstruksjoner. Disse går historisk tilbake til de klassiske problemene som har med sirkelens kvadratur, kubens fordobling og vinkelens tredeling å gjøre.

Kvadratroten av 2 er lik med hypotenusen til en rettvinklet trekant med sidekanter lik 1 og er derfor et konstruerbart tall.

Gitt to punkter i planet, kan disse forbindes med en rett linje. På dette linjestykket kan ved en geometrisk konstruksjon basert på transversalteoremet settes av et endelig antall, ekvidistante punkter. Hvert slikt punkt vil ha en avstand fra endepunktet til det gitte linjestykket som er en viss brøkdel av dette og tilsvarer derfor et rasjonelt tall. Slike ekvidistante punkt kan på samme måte legges ut i andre retninger og punktene i dette euklidske planet vil derfor ha koordinater som er rasjonelle tall og utgjør tallkroppen Q.

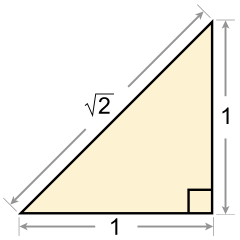
Ved en geometrisk konstruksjon som vist i figuren, kan man også konstruere kvadratrøtter som for eksempel √2. Dette er ikke lenger et rasjonelt tall, men irrasjonelt. Det gir opphav til en ny lengde som vil tilsvare punkter med koordinater av formen a + b√2 hvor både a og b er rasjonelle. Disse nye tallene tilhører en utvidelse av tallkroppen Q og betegnes ved Q(√2). Da en kvadratrot tilsvarer løsningen av en andregradsligning, sies denne utvidelsen av Q å være av andre grad.

Benytter man disse nye punktene i videre, geometriske konstruksjoner som involverer kvadratrøtter, vil det igjen gi nye punkt med koordinater i en tallkropp med den dobbelte grad, det vil en med grad 4 = 2² over utgangskroppen Q. Slik kan man fortsette og dermed bygge opp tallkropper med grad 2^m over den opprinnelige. Denne sammenhengen mellom geometriske konstruksjoner og tallteori ble først forstått av Carl Friedrich Gauss rundt 1800 og bevist av Pierre Wantzel vel tredve år senere. Dette åpnet opp et nytt, matematisk felt som også var intimt forbundet med Niels Henrik Abels arbeid rundt løsning av polynomligninger og dets videreføring av Evariste Galois. I dag blir ofte alt dette omtalt som en del av moderne Galois-teori.

Aritmetiske regneoperasjoner

For at to konstruerbare tall a og b skal tilhøre en tallkropp må de kunne kombineres ved de fire aritmetiske regneoperasjonene addisjon, subtraksjon, multiplikasjon og divisjon ved geometriske konstruksjoner. De to første kan enkelt utføres ved å forlenge eller forminske linjestykket med lengde a med en lengde b. Dette kan alltid gjøres ifølge de fundamentale aksiomene i euklidsk geometri.

Multiplikasjon

Geometrisk multiplikasjon av a og b.

Tallet a og vil tilsvare et linjestykke OA i figuren. Gjennom punktet O trekkes en vilkårlig linje. På den settes av et punkt P slik at lengden av linjestykket OP tilsvarer den lengdeenheten man har valgt å bruke. Videre settes av på samme linje et punkt B slik at OB har lengden b som er den andre faktoren i multiplikasjonen. Punktene A og P forbindes med en linje. En ny linje konstrueres så gjennom punktet B slik at den er parallell med AP. Den skjærer forlengelsen av OA i et punkt C. Lengden av linjestykket OC  er nå produktet c = ab.

Bevis for dette resultatet følger fra transversalteoremet. Det sier at OC/OA = OB/OP  som betyr at c/a = b  som gir c = ab. Dette argumentet er ekvivalent med å benytte at trekantene OAP og OCB er likeformete da linjestykkene AP og CB er parallelle.

Divisjon

Geometrisk divisjon av to tall a og b.

Divisjonen a/b utføres geometrisk ved å merke av de tilsvarende linjestykkene på samme måte som ved multiplikasjon. Men nå forbindes punktene A og B med en linje. Gjennom punktet P trekkes en ny linje som er parallell med denne. Den skjærer linjen gjennom O og A i et nytt punkt C. Linjestykket OC har nå lengden c = a/b  som er det ønskede resultatet.

Igjen sees fra figuren at OC/OP = OA/OB som gir direkte resultatet c = a/b  av divisjonen. Det følger fra at trekantene OCP og OAB er likeformete da linjestykkene CP og AB er parallelle med hverandre.

Kvadratrot

Geometrisk konstruksjon av kvadratroten til produktet av to tall.

Kvadratroten av et produkt ab  av to tall a og b kan konstrueres geometrisk ved å merke av de tilsvarende linjestykkene på en linje ut fra et punkt O som vist i figuren til venstre. Velges for eksempel a å være lengdeenheten som man ønsker å benytte, vil konstruksjonen derfor gi kvadratroten av b.

Selve kvadratroten kommer frem ved å konstruere en sirkel som har linjestykket AB som diameter. Gjennom punktet O trekkes en rett linje vinkelrett på AB. Den skjærer den øvre halvsirkelen i punktet C. Linjestykket OC  har nå lengden c = √(ab).

Beviset for dette bygger på halvsirkelteoremet. Dette sier at vinkelen C i trekanten ABC er en rett vinkel. Trekantene AOC og COB er derfor likeformete da deres hjørnevinkler er like store. Det betyr at AO/OC = OC/OB eller a/c = c/b slik at c² = ab. Herav følger så resultatet som sier c er det geometrisk gjennomsnittet av a og b.

Kroppsutvidelse

Hvis man betrakter et tall k som tilhører den rasjonelle tallkroppen Q, og konstruer dets kvadratrot √ k, så vil dette nye tallet ikke lenger tilhøre tallkroppen Q. Derimot vil det tilhøre en utvidet tallkropp K₁ = Q(√ k ) som består av tall av formen a + b√ k hvor både a og b er rasjonelle tall. Disse tallene er røtter i en andregradsligning, og man sier at utvidelsen er av andre grad. Det skrives som [K₁ : Q] = 2.

Ved en ny, geometrisk konstruksjon basert på punkt som har koordinater i tallkroppen K₁ og gir nye punkt som er skjæringspunkt mellom to sirkler eller en linje og en sirkel, vil de nye punktene tilhøre en neste kroppsutvidelse K₂ = K₁(√ k₁ ) bestående av tall på den generelle formen a₁ + b₁√ k₁ hvor a₁, b₁ og k₁ tilhører K₁. Dette er igjen en utvidelse av K₁ av andre grad eller [K₂ : K₁] = 2. På den måten får man konstruert tall som består av nøstede uttrykk med kvadratrøtter. For eksempel, så vil tallet

$5{\sqrt {2}}+7{\sqrt {3+{\sqrt {2}}}}$

tilhøre kroppen K₂. Det vil være rot i en spesiell fjerdegradsligning med koeffisienter fra kroppen Q. Det tilsvarer at utvidelsen er av fjerde grad over de rasjonelle tallene, det vil si [K₂ : Q] = [K₂ : K₁]⋅[K₁ : Q] = 4.

Fortsetter man videre på samme måte vil man etter m konstruksjoner komme frem til tall som tilhører en kropp K_m av grad [K_m : Q] = 2^m over de rasjonelle tallene. De kan igjen skrives som rasjonelle uttrykk med et endelig antall nøstede kvadratrøtter. Alle konstruerbare tall vil tilhøre en slik tallkropp.

Regulære polygoner

Den enkleste, regulære mangekant er en tokant eller 2-gon hvor de to sidene er sammenfalt til en diameter i den omskrevne sirkelen. Halveres nå sentralvinkelen α₂ = π, fremkommer to nye punkter på sirkelen som sammen med de opprinnelig utgjør en regulær firkant eller kvadrat. Dette har sidekant s₄ = √2 hvis radius i den omskrevne sirkelen er 1. Hele omkretsen til kvadratet er p₄ = 4√2. Disse lengdene tilhører tallkroppen K₁.

Hvis man så igjen halverer de nye sentralvinklene med størrelse α₄ = π/2 fremkommer på samme måten en 8-kant eller regulær oktagon. En enkel beregning basert på Pythagoras' læresetning gir da at den har en sidekant med lengde s₈ = √(2 - √2) og omkrets p₈ = 8s₈. Disse konstruerte tallene tilhører kroppen K₂.

Slik kan man fortsette til man har en n-gon som har sidekanter med lengden s_n = 2 sin(π/n). Etter nok en halvering av siden får man en 2n-gon med sidekant s_2n. Ved nå å bruke den trigonometrisk formelen

$\sin \alpha ={\sqrt {1-\cos {2\alpha } \over 2}}$,

finner man sammenhengen

$s_{2n}={\sqrt {2-{\sqrt {4-s_{n}^{2}}}}}$

mellom sidelengdene før og etter delingen. Dette er en rekursiv relation med startverdien s₄ = √2. Etter m halveringer har man en mangekant med n = 2^m+1 sidekanter. Disse har lengden

$s_{n}=\underbrace {\sqrt {2-{\sqrt {2+{\sqrt {2+{\sqrt {2+\cdots +{\sqrt {2}}}}}}}}}} _{m}$.

hvor man på høyresiden har m nøstede kvadratrøtter av 2. Denne sidelengden er nå et konstruerbart tall og tilhører tallkroppen K_m.

Omkretsen eller periferien til mangekanten er p_n = ns_n. I grensen hvor sidetallet n blir veldig stort, vil den nærme seg verdien 2π  for en sirkel med readius lik 1. På den måten kommer man frem til uttrykket

$\pi =\lim _{m\to \infty }2^{m}\underbrace {\sqrt {2-{\sqrt {2+{\sqrt {2+{\sqrt {2+\cdots }}}}}}}} _{m}$

for konstanten π. Det tilsvarer resultatet som den franske matematiker François Viète fant på 1500-tallet. Denne versjonen er litt enklere da den ikke involverer et produkt av et stort antall faktorer. Velger man her m = 6, finner man π = 3,1413... som har tre korrekte desimaler.

Syklotomisk tallkropp

Hjørnene til en regulær n-kant har i det komplekse planet koordinatene z_k = e^{2π i k/n} med k = 0,1,2,..,n - 1. De er løsninger til sirkeldelingsligningen xⁿ - 1 = 0 som også blir kalt for den syklotomiske ligningen. Sammen utgjør de en basis for en syklotomisk tallkropp med dimensjon eller grad gitt ved Eulers totientfunksjon φ(n).

Polygonene som kommer frem ved halveringer av sidene av den opprinnelige tokanten, har n = 2^m+1 sidekanter etter m halveringer. Da den aritmetiske φ-funksjonen har egenskapen φ(p^r) = p^{r - 1}(p - 1) når p er et primtall, betyr det at graden til tallkroppen tilsvarende disse polygonene er φ(n) = 2^m. Og det er i full overensstemmelse med hva som allerede er funnet for graden til tallkroppen K_m  ut fra kravet om at den skulle inneholde konstruerbare tall.

Hvis man i stedet for en tokant hadde startet sidehalveringen med en regulær trekant, ville man på tilsvarende måte ha kommet frem til en polygon med n = 3⋅2^m sider etter m slike halveringer. Da Eulers totientfunksjon har egenskapen φ(pq) = φ(p)φ(q) når tallene p og q er relativt primisk, vil den tilsvarende syklotomiske tallkroppen få samme grad 2^m ved å benytte at φ(p) = p - 1 når p er et primtall. Hjørnene i disse regulære mangekantene er derfor som ventet også konstruerbare. Det samme gjelder hvis man starter med en regulær femkant. Den krever en mer komplisert konstruksjon og dens hjørnepunkter tilhører en syklotomisk tallkropp av grad φ(5) = 4 = 2².

En regulær 7-gon lar seg derimot ikke konstruere geometrisk da φ(7) = 6 ikke kan skrives som en potens av 2. På samme måte kan heller ikke en 9-kant konstrueres da φ(9) = φ(3²) = 3⋅2 heller ikke er en potens av 2. Mer generelt, for et primtall p vil den tilsvarende p-gon ha muligheten å la seg konstruere geometrisk kun hvis φ(p) = p - 1 = 2^r der eksponenten r er et positivt heltall. Det vil si at p = 2^r + 1. Men betingelsen at p skal være primtall, medfører at tallet r må ha formen r = 2^k hvor k også er et heltall. Resultatet er derfor at for en p-gon skal kunne konstrueres geometrisk må p være et av Fermat-tallene

$F_{k}=2^{2^{k}}+1,\;\;k=0,1,2,\ldots$

Men bare de fem første av disse er primtall, F₀ = 3, F₁ = 5, F₂ = 17, F₃ = 257 og F₄ = 65537. På samme måte som en 9-gon ikke kan konstrueres geometrisk, kan heller ikke polygoner med sidetall som inneholder to eller flere av det samme Fermat-tallet som faktorer. Hvis så disse halveres, oppstår nye, regulære mangekanter. De vil alle ha et antall sidekanter som generelt kan skrives som

$n=2^{m}F_{0}^{\nu _{0}}F_{1}^{\nu _{1}}F_{2}^{\nu _{2}}F_{3}^{\nu _{3}}F_{4}^{\nu _{4}}$

hvor eksponentene til Fermat-tallene kun kan ta verdiene ν_i = 0,1. Det gir i alt 31 konstruerbare polygoner med et odde antall sidekanter.

Denne forståelsen av de regulære mangekantene ble først gitt av Carl Friedrich Gauss på begynnelsen av 1800-tallet i han banebrytende verk Disquisitiones Arithmeticae. Vel tyve år senere ble teorien for løsningene av mer generelle, polynomligninger videre utviklet av Niels Henrik Abel og Evariste Galois. Noe senere fant Pierre Wantzel betingelsene som måtte være oppfylt for å finne slike løsninger ved geometriske konstruksjoner.

Litteratur

• J. Reed og J. Aarnes, Matematikk i vår tid, Universitetsforlaget, Oslo (1967).
• S. Thorvaldsen, Matematisk kulturhistorie, Eureka Forlag, Høgskolen i Tromsø, Tromsø (2003). ISBN 82-7389-045-7.
• R. Courant and H. Robbins, What is Mathematics?, Oxford University Press, Oxford (1996). ISBN 0-195-10519-2.

Eksterne lenker

• E.W. Weisstein, Constructible Number, Wolfram MathWorld.