Bølge
En bølge er en forstyrrelse eller utslag som sprer seg gjennom rommet med konstant hastighet og dermed overfører energi. Mens lydbølger og vannbølger brer seg i et medium, kan elektromagnetisk stråling og gravitasjonsbølger spre seg gjennom vakuum med lyshastigheten.
De fleste bølger lar seg klassifisere som «longitudinalbølger» eller «transversalbølger» avhengig av om utslaget er langs eller vinkelrett på utbredelsesretningen. En lydbølge i en gass er longitudinal, mens en elektromagnetisk bølge er transversal. Lydbølger i et fast stoff kalles for seismiske bølger og er en blanding av både transversal og longitudinal bevegelse.
Utbredelsen til alle bølger beskrives ved en bølgeligning. For bølger med en konstant utbredelseshastighet, har denne vanligvis samme, matematiske form og beskriver «ikke-dispersive bølger». Når dette ikke er tilfelle, snakker man om «dispersive bølger». Havbølger er et viktig eksempel på slike. Mer abstrakte bølger av denne typen benyttes i kvantemekanikken og deres utbredelse er gitt ved Schrödingerligningen.
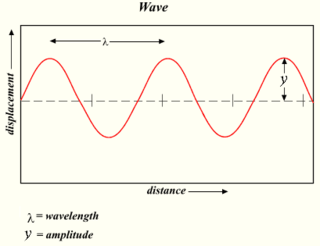
Spesielt viktig er harmoniske bølger hvor forstyrrelsen i hvert punkt i rommet varierer med tiden som for en harmonisk oscillator. En slik bølge har derfor en bestemt frekvens og får dermed også en bestemt bølgelengde. Den har en form i tid og rom som er gitt ved en sinuskurve. En hvilken som helst annen bølge kan fremstilles som en sum (eller integral) av harmoniske bølger, hver med sin egen frekvens. Dette danner grunnlaget for Fourier-analysen som er av meget stor betydning innen fysikk og teknologi.
Bølgeligningen
redigerUtbredelsen av en bølge er beskrevet ved bølgeligningen. Vanligvis tenker man seg en bølge med uendelig utstrekning, men den kan også bestå av en enkel forstyrrelse eller «bølgepakke» som brer seg utover med konstant hastighet. Et typisk eksempel er en havbølge med form av en tsunami. Beveger bølgen seg i en dimensjon, vil den matematisk være beskrevet ved en funksjon F(t,x) hvor t er tiden og x koordinaten i utbredelsesretningen. Er v bølgens hastighet, vil en person som forflytter seg med samme hastighet, oppleve å se at bølgeformen ikke forandrer seg med tiden. Da denne observatøren har koordinaten x' , vil han derfor si at bølgen er beskrevet ved en konstant funksjonen f (x' ). Men nå er x' = x - vt hvis observatøren begynner sin reise ved tidspunktet t = 0. Derfor er bølgen beskrevet ved «bølgefunksjonen» F = f (x - vt) når den beveger seg i positiv x-retning.[1] Hadde den beveget seg i motsatt retning, ville man benytte en funksjon F = g (x + vt). Argumentet x ± vt kalles bølgens fasefunksjon og størrelsen v blir da mer nøyaktig omtalt som fasehastigheten.
De aller fleste bølger «lineære» i den forstand at hvis to kilder forårsaker bølgene F1(t,x) og F2(t,x), så vil den totale forstyrrelsen i punktet x ved tidspunktet t være F1(t,x) + F2(t,x). Dette gir opphav til interferens som er en fundamental egenskap ved all bølgebevegelse. Det betyr at når bølgene F1 og F2 oppfyller bølgeligningen, må også summen F = F1 + F1 oppfylle den.
Som alle andre bevegelsesligninger må også bølgeligningen være en differensialligning som inneholder deriverte med hensyn på de to variable t og x. Denne ligningen kan finnes ved å betrakte den resulterende bølgen
som oppstår i møtet mellom to motgående bølger. Ved å innføre u1 = x - vt og u2 = x + vt, blir da ∂F/∂x = f 1' + f 2' og ∂F/∂t = - v f 1' + v f 2' hvor apostrofen betyr den deriverte med hensyn på det ene argumentet u1 eller u2. For dispersive bølger kan man ikke finne noen generell forbindelse mellom disse to partiellderiverte som er avhengig av bølgeformene f 1 og f 2. Derimot hvis utbredelseshastigheten til bølgene er uavhengig av deres form, vil de tilsvarende andrederiverte ∂2F/∂t 2 og ∂2F/∂x 2 være forbundet ved sammenhengen[2]
Dette er bølgeligningen i en dimensjon for en ikke-dispersiv bølge. For en bølge F(t,x,y,z) som kan bre seg ut i tre dimensjoner med samme hastighet i alle retninger, vil da bølgeligningen bli
Kombinasjonen av partiellderiverte inni parentesen er Laplace-operatoren. Den kan skrives mer kompakt ved bruk av nabla-symbolet slik at bølgeligningen i tre dimensjoner kan skrives på den alternative formen
Denne partielle differensialligningen for en svingende streng ble først utledet av Jean le Rond d'Alembert på midten av 1700-tallet. Kort tid etterpå fant Leonhard Euler bølgeligningen i tre dimensjoner.[3]
Harmoniske bølger
redigerFormen til en bølge som beveger seg til høyre langs x-aksen, er gitt ved bølgefunksjon f(u) hvor u = x - vt. Når denne funksjonen er en sinuskurve, sies bølgen å være harmonisk. Da er f(u) = A cos(k(x - vt)) hvor konstanten A kalles amplituden til den harmoniske bølgen og konstanten k er dens bølgetall. Betrakter man bølgen ved et gitt tidspunkt t0, vil da utslaget variere som A cos(kx - φ0) hvis man skriver φ0 = kvt0. Det vil derfor være det samme i et punkt x som i et punkt x + λ hvor kλ = 2π da sinusfunksjonen er periodisk med periode 2π . Dette gir sammenhengen
mellom bølgetallet k og bølgelengden λ. Ved et gitt tidspunkt er derfor utslaget til bølgen det samme i alle punkt med en gjensidig avstand som er et helt antall bølgelengder.
På samme måte, hvis man betrakter bølgen i et punkt x0 i rommet, så vil utslaget der variere som A cos(kvt - θ0) der θ0 = kx0. Det tilsvarer at i dette punktet varierer utslaget harmonisk med vinkelfrekvensen
Den normale frekvensen f = ω/2π er derfor relatert til bølgelengden ved den viktige sammenhengen
som kan betraktes som en definisjon av fasehastigheten. Her er den like stor som bølgehastigheten.
Bølgefunksjonen for en harmonisk bølge som beveger seg mot høyre, kan nå skrives på den generelle formen
hvor fasevinkelen φ avhenger av hvordan bølgen ser ut ved tidspunktet t = 0. Vanligvis kan denne settes lik null. Men hvis flere slike bølger opptrer samtidig, er disse relative fasevinklene avgjørende som ved interferens.
Stående bølger
redigerHarmoniske bølger kan klassifiseres i to hovedtyper. Enten beveger de seg med jevn hastighet eller så svinger de synkront om samme likevektsposisjon. En bølge av den ene typen kan uttrykkes som en kombinasjon av bølger av den andre typen. Det ser man fra uttykket som beskriver bølgen som beveger seg mot høyre. Det kan omformes til
når man benytter den trigonometriske identiteten som uttrykker cosinus til en differanse av to vinkler ved sinus og cosinus til hver av vinklene. Hvert av de to leddene her på høyre side representerer en stående bølge hvor alle punktene svinger synkront «i fase». Det betyr at hvert punkt på bølgen når sitt maksimale utslag samtidig, og alle punktene går samtidig gjennom likevektsposisjonen med null utslag.[4]
En slik stående bølge vil alltid ha punkter som ikke beveger seg i det hele tatt. Disse kalles noder eller «knuter». For eksempel, den stående bølgen
kan derfor også betraktes som en kombinasjon av to motgående bølger med motsatt like store amplituder. Den har noder i punktene bestemt ved kxn = nπ hvor n = 0,1,2,3, etc. Ved å innføre bølgelengden λ = 2π/k, kan lokaliseringen til nodene skrives xn = nλ/2.
Stående bølger benyttes til å gi musikkinstrumenter bestemte toner. Mens en svingende streng har noder der den blir holdt fast og dermed ikke kan svinge, vil luftsøylen i et blåseinstrument ha noder som er bestemt ved ventilenes plassering. Ved å åpne og lukke disse, eksiteres forskjellige stående bølger som gir musikalske toner.
Plane bølger
redigerDen harmoniske bølgen F(t,x) = A cos(kx - ωt) kan også betraktes som en plan bølge som beveger seg mot høyre og fyller hele rommet. Ved et gitt tidspunkt er da utslaget det samme i hvert plan x = konstant. Alternativt kan den skrives som F(t,x) = A cos(k⋅x - ωt) når man innfører bølgevektoren som her er k = k ex og viser at bølgen beveger seg langs x-aksen angitt ved enhetsvektoren ex. Bølgevektoren står vinkelrett på bølgefronten som her er et plan. Den kalles derfor også ofte for bølgenormalen. Alle punkt i bølgefronten har samme fase.
En slik plan bølge
med samme bølgetall, men som beveger seg i en vilkårlig retning gitt ved enhetsvektoren n, vil ha en fast bølgevektor k = k n = (kx, ky, kz). Ved et gitt tidspunkt vil den ha samme utslag i alle punkt i rommet som ligger på planet k⋅x = kxx + kyy + kzz = konstant. Dette planet beveger seg med konstant hastighet v i retning av bølgevektoren k. Den er en løsning av den tredimensjonale bølgeligningen når betingelsen
er oppfylt. Størrelsen til bølgevektoren er derfor fremdeles gitt ved bølgetallet k = |k| = 2π /λ.
I mange sammenhenger er det praktisk å beregne egenskaper ved bølger som om utslagene kunne ta komplekse verdier. Ved bruk av Eulers formel kan man da skrive en plan bølge som
hvor man tar «realdelen» av den komplekse eksponensialfunksjonen. Ofte er dette underforstått slik at bølgefunksjonen skrives uten at Re angis. Den sies da å være gitt som en kompleks fasevektor. Mange forskjellige beregninger kan dermed forenkles.[5]
Dispersive bølger
redigerNår lys beveger seg gjennom et materiale med brytningsindeks n, er fasehastigheten v = ω/k = c/n hvor c er lyshastigheten i vakuum. Lyset blir dermed brutt ved at det blir splittet opp i sine forskjellige spektrale komponenter, hver med sin farge. Det skyldes at brytningsindeksen er en funksjon av bølgelengden λ og fenomenet omtales som dispersjon. Da k = 2π/λ, betyr det derfor at vinkelhastigheten er en funksjon ω(k) som ikke lenger er lineær som i vakuum. En slik bølge sies derfor å være «dispersiv».
Dispersive bølger oppfyller ikke den vanlige bølgeligningen da hver frekvenskomponent vil bevege seg med forskjellig fasehastighet. I stedet er de beskrevet ved mer kompliserte ligninger som også kan være ikke-lineære. Slike bølger kan kombineres til bølgepakker som beveger seg med gruppehastigheten vg = ∂ω/∂k. Dette er også den hastigheten som energien til bølgen forplanter seg med. I kvantemekanikken brukes slike bølgepakker til å beskrive en lokalisert partikkel hvis hastighet er lik med gruppehastigheten til bølgene den består av.
Vannbølger
redigerSe egne artikkel om havbølge.
Bølger i vann er beskrevet ved Euler-ligningene. De er meget komplisert og kan ikke generelt løses eksakt. Det tilsvarer at en nøyaktig beskrivelse av for eksempel havbølger alltid har vært en stor utfordring. Men ved små bølgebevegelser kan ligningene lineæriseres og dermed løses på en forhåldsvis enkel måte.[6] For en bølge som beveger seg langs x-aksen er da bølgehøyden
hvor amplituden A karakteriserer bølgens energi. Er dypden til vannet D, har denne bølgen fasehastigheten
hvor g er tyngdeakselerasjonen. Vannbølger er derfor i alminnelighet dispersive. Mer nøyaktige beregninger gir korreksjoner til dette laveste ordens resultat.
Der er to hovedklasser av vannbølger avhengig av hvor stor bølgelengden λ = 2π/k er i forhold til dybden D. Når λ << D, kan man sette tanh kD = 1 i uttrykket for fasehastigheten som dermed blir v = √(g/k). Man snakker da om dype bølger som har en fasehastighet som øker med bølgelengden. Det kan man observere ved å kaste en sten ut i et vann. Da blir det dannet bølger med mange forskjellige bølgelengder. Etter kort tid vil man se at de med størst bølgelengde beveger seg raskest bort fra sentrum.
I den motsatte grensen λ >> D er dypden mye mindre enn bølgelengden og man har grunne bølger. Da kan man sette tanh kD = kD i formelen for fasehastigheten slik at den blir v = √(gD). Den er derfor uavhengig av bølgelengden slik at grunne bølger ikke er utsatt for dispersjon i denne tilnærmelsen. Eksempel på bølger av denne typen er en tsunami som er en bølge med meget stor bølgelengde. Blir den skapt langt ute i havet som kan være flere kilometer dypt, vil den kunne bevege seg med en hastighet som blir flere hundre kilometer i timen, det vil si omtrent så raskt som et fly.
Kvantemekanikk
redigerMens fysiske bølger er beskrevet ved reelle bølgefunksjoner, benyttes komplekse bølgefunksjoner Ψ = Ψ(t,x) i kvantemekanikken til å beskrive partikler. Disse har i seg selv ingen direkte fysisk betydning, men produktet Ψ*Ψ angir sannsynligheten for å finne en partikkel i punktet x ved tidspunktet t. Her er Ψ* den komplekskonjugerte av funksjonen Ψ. Disse abstrakte bølgene omtales ofte som materiebølger og er beskrevet ved Schrödinger-ligningen. For en fri partikkel med masse m er den
hvor i = √-1 er den imaginær enhet og er Planck-Dirac-konstanten. Denne bølgeligningen har en annen form da disse bølgene ikke uten videre kan tilordnes en bestemt fasehastighet slik at de i alminnelighet er dispersive.
Den plane bølgen
er den enkleste løsningen av Schrödinger-ligningen.[7] Her er igjen k bølgevektoren og ω er vinkelfrekvensen som ikke lenger er forbundet via en konstant bølgehastighet. Derimot er partikkelens impuls gitt som og dens energi som nå i stedet oppfyller den klassiske sammenhengen .
For denne løsningen av Schrödinger-ligningen er produktet Ψ*Ψ uavhengig av posisjonen x til partikkelen. Det betyr at når den har en bestemt impuls p, er sannsynligheten den samme for å finne den i hvilket som helst punkt i rommet. Dette er et uttrykk for Heisenbergs uskarphetsrelasjon som gjør kvantemekanikk så vanskelig å sammenholde med klassisk fysikk.
En mer lokalisert partikkel beskrives ved en bølgepakke. Dens gruppehastighet er lik med den klassiske hastigheten v = p/m. I motsetning til den tidligere beskrivelsen av partikkelen som en plan bølge, vil denne bølgepakken inneholde mange forskjellige impulskomponenter sentrert rundt den klassiske verdien p slik at Heisenbergs uskarphetsrelasjon fortsatt er oppfylt.
Sfæriske bølger
redigerMens en sten som kastes ut i et vann, forårsaker bølger som brer seg radielt utover med bølgetopper som danner sirkler, vil en lydkilde skape lydbølger som brer seg utover i luften med bølgetopper som danner kuleflater. Disse bølgene kalles «sfæriske bølger» eller kulebølger og har mange praktiske anvendelser.
De beskrives mest naturlig ved bruk av kulekoordinater slik at den generelle bølgefunksjonen for en harmonisk bølge har formen F(t,x) =U(r,θ,φ) cosωt. Innsatt i den vanlige bølgeligningen vil derfor den romlige delen av funksjonen måtte oppfylle
hvor bølgetallet k = ω/v. Dette er Helmholtz-ligningen. For de mest symmetriske bølgene avhenger denne funksjonen bare av den radielle variable r. Ved å benytte Laplace-operatoren i kulekoordinater, kan da ligningen forenkles til[5]
Funksjonen rU oppfyller derfor svingeligningen for en harmonisk oscillator slik at den generelle løsningen har formen
Den beskriver i alminnelighet en sum av «inngående» og «utgående» kulebølger av formen (1/r) cos(kr ± ωt). Kan utslaget ta komplekse verdier, vil den utgående bølgen ha formen[7]
når den har en gitt frekvens. Mer generelt vil den kunne skrives som
når c er fasehastigheten og f(r) er en vilkårlig funksjon. Amplituden avtar derfor med avstanden fra kilden. På samme måte forklares blant annet hvorfor signalet fra en radiosender blir svakere etterhvert som man beveger seg bort fra den. Dette kan forstås ved at energien som sendes ut i bølger, spres over et stadig større område slik at intensiteten gradvis svekkes.
Se også
redigerReferanser
rediger- ^ N.P. Callin, C.W. Tellefsen, S. Haagensen, J. Pålsgård og R. Stadsnes, ERGO Fysikk 2, Aschehoug, Oslo (2008). ISBN 9788203337208.
- ^ J.B. Marion and W.F. Hornyak, Physics for Sciences and Engineering, Holt-Saunders International Editions, New York (1982). ISBN 4-8337-0098-0.
- ^ M. Kline, Mathematical Thought from Ancient to Modern Times, Volume 2, Oxford University Press, England (1972). ISBN 0-19506136-5.
- ^ H.D. Young and R.A. Freedman, University Physics, Addison Wesley, New York (2008). ISBN 978-0-321-50130-1.
- ^ a b D.J. Griffiths, Introduction to Electrodynamics, Prentice Hall, New Jersey (1999). ISBN 0-13-805325-X.
- ^ B. Lautrup, Physics of Continuous Media, IOP Publishing Ltd, Bristol (2005). ISBN 0-7503-0752-8.
- ^ a b R.A. Serway, C.J. Moses and C.A. Moyer, Modern Physics, Saunders College Publishing, Philadelphia (1989). ISBN 0-03-004844-3.
Eksterne lenker
rediger- (en) Waves – kategori av bilder, video eller lyd på Commons
- (en) Wave – galleri av bilder, video eller lyd på Commons
- Arnt Inge Vistnes, Svingninger og bølger, forelesninger i FYS2130, Universitetet i Oslo (2016).
- BCAM, History of waves Arkivert 31. august 2021 hos Wayback Machine., historisk fremstilling.