Kvantisert harmonisk oscillator
Kvantisert harmonisk oscillator er den kvantemekaniske beskrivelsen av en klassisk, harmonisk oscillator. Historisk var denne den første anvendelsen av moderne kvantemekanikk som Werner Heisenberg kunne gjøre. Senere fikk den en grunnleggende rolle i all kvantefeltteori som kan bygges opp som uendelig mange slike oscillatorer.
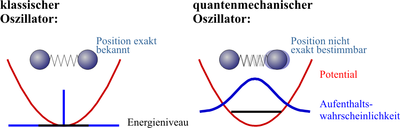
Den harmoniske oscillatoren er ett av de få systemer i kvantemekanikken som lar seg løse eksakt. I tillegg er det spesielt at dette gjelder både når oscillatoren svinger i én eller i flere dimensjoner. Da de fleste andre kvantefysiske problem ikke lar seg løse på den måten, vil likevel en harmonisk oscillator ofte kunne gi en god approksimasjon. Korreksjoner til denne første tilnærmelsen kan så beregnes på en systematisk måte.
En kvantemekanisk partikkel i et oscillatorpotensial skiller seg i størst grad fra en tilsvarende klassisk partikkel ved at det er umulig for den å ligge i ro på bunnen av potensialet. Det skyldes Heisenbergs uskarphetsrelasjon som sier at hvis partikkelens posisjon er kjent, vil den bevege seg med stor hastighet.
Algebraisk metode rediger
En harmonisk oscillator betegner en partikkel som beveger seg i et potensial som øker med kvadratet av avstanden fra et senter. Den kvantemekaniske beskrivelsen er basert på Hamilton-operatoren som kan finnes fra det klassiske uttrykket for energien til partikkelen. Hvis den har masse m og oscillerer med vinkelfrekvens ω, er derfor dens bevegelse gitt ved Hamilton-operatoren
når man betrakter det enkleste tilfellet der partikkelen kun kan bevege seg i én dimensjon.[1]
De viktigste egenskapene til dette systemet er gitt ved dets stasjonære tilstander og tilsvarende egenverdier for energien. En grunn til at den harmoniske oscillatoren er så viktig, er at disse kan finnes ved en ren algebraisk fremgangsmåte. Den er i praksis den samme som Heisenberg benyttet i sin første løsning av dette problemet.
Stigeoperatorer rediger
Hamilton-funksjonen til partikkelen er dens klassiske energi uttrykt ved koordinaten q og impulsen p. Siden den er kvadratisk i begge disse størrelsene, kan man på et vis ta dens «kvadratrot» ved å skrive den som et produkt av to komplekse variable ved å innføre den imaginære enheten i = √-1. Denne faktoriseringen gjør det naturlig å innføre operatoren
i den kvantemekaniske Hamilton-operatoren. Sammen med den hermitisk adjungerte operatoren
gir nå produktet
Ved bruk av den kanoniske kommutatoren kan Hamilton-operatoren skrives som
Direkte utregning fra den samme kommutatoren finner man også
som viser at disse to operatorene er stigeoperatorer. Derfor er en antallsoperator med heltallige egenverdier n = 0, 1, 2 og så videre. Det gir resultatet
for de kvantiserte energinivåene til oscillatoren. Den laveste verdien er E0 = (1/2)ħω som er dens «nullpunktsenergi». Over denne grunntilstanden ligger eksiserte nivå i samme avstand ħω fra hverandre.[1]
Nullpunktsenergi rediger
Klassisk ville partikkelen ligge i ro i bunnen av det harmoniske potensialet og dermed ha null energi. Grunnen til at den kvantiserte oscillatoren alltid har større energi, skyldes Heisenbergs uskarphetsrelasjon For et utslag q, må derfor impulsen Det betyr at energien til oscillatoren må oppfylle betingelsen
Funksjonen på høyre side har et minimum for et visst utslag. Ved derivasjon finnes det å opptre for Innsatt i funksjonen gir det den minimale energien
Nødvendigheten av en slik nullpunktsenergi i grunntilstanden hadde tidligere vært diskutert i forskjellig andre sammenhenger, men det var Heisenbergs kvantisering som etablerte den med sikkerhet. I dag tilsvarer grunntilstanden for oscillatoren vårt fysiske vakuum hvor nullpunktsenergien opptrer i Casimir-effekten og kan spille en rolle som «sort energi» i kosmologisk sammenheng.[2]
Egentilstander rediger
Egenverdiene til antallsoperatoren gir antall kvant eller eksitasjoner n som finnes i en stasjonær tilstand Denne er en egentilstand og oppfyller
Grunntilstanden er per definisjon ikke eksistert og inneholder n = 0. Den må derfor tilfredsstille Det følger også fra at er en «senkeoperator» som ikke kan redusere antall kvant lavere enn til null.
Eksisterte tilstander kan bygges opp ved bruk av «heveoperatoren» Det gir første eksiterte nivå Gjentatt bruk gir høyere eksisterte nivå. Da kan man benytte at for alle slike stigeoperatorer av denne typen gjelder sammenhengene
som kan verifiseres ved bruk av den fundamentale kommutatoren.[3]
En vilkårlig tilstand kan dermed skrives som
Den er automatisk normerert som når grunntilstanden er normert slik.
Tidsutvikling rediger
De harmoniske svingningene til oscillatoren kan beskrives i Heisenberg-bildet ved å finne hvordan dens forskjellige operatorer forandrer seg med tiden. I praksis er det bestemt av tidsutviklingen til de to stigeoperatorene. Den er styrt av Heisenbergs bevegelsesligninger
Begge ligningene kan løses enkelt fra definisjonen av eksponentialfunksjonen og gir
Posisjonsoperatoren til den oscillerende partikkelen varier nå som
Dette resultatat har samme form som den klassiske svingningen Denne formen fremkommer når man lar de kvantemekaniske stigeoperatorene ble de komplekse variable og der θ er en fasevinkel som er bestemt av posisjonen ved tiden t = 0.
Bølgefunksjoner rediger
Mens egentilstandene til oscillatoren er ket-vektorer i et Hilbert-rom med uendelige dimensjoner, er bølgefunksjone
rent formelt projeksjoner av disse vektorene på en koordinatbasis i det samme rommet. Det medfører at impulsoperatoren kan representeres ved en vanlig derivasjonsoperator, Dette gjør det mulig å bestemme bølgefunksjonen for grunntilstanden på en direkte måte fra definisjonen av den tilsvarende ket-vektoren. Den betyr at og gir dermed den enkle differensialligningen
Løsningen kan uttrykkes ved funksjonen som beskriver Gauss-kurven. Hvis man samtidig vil at den skal ha normeringen
som følger fra kravet og bruk av Gauss-integralet, er grunntilstanden beskrevet ved bølgefunksjonen
Funksjonen har et maksimum i posisjon q = 0. Det er det mest sannsynlige sted partikkelen kan finnes når systemet er i grunntilstanden. I tillegg er det posisjonen til den klassiske partikkelen når den ligger i ro.[3]
Eksiterte energinivå rediger
Kvantetilstandene med høyere energi har bølgefunksjoner som også kan finnes fra definisjonen av de tilsvarende egenvektorene. Den gir
når man introduserer den nye variable x = q √(mω /ħ). Dermed kan disse egenfunksjonene skrives på formen
når de uttrykkes ved de spesielle Hermite-polynomene
De åtte første er
Bølgefunksjonene er derfor vekselvis symmetrisk og antisymmetrisk om origo x = 0. De har like mange nullpunkter som eksitasjonstallet n eller antall kvant i tilstanden.
Schrödinger-ligning rediger
Omtrent for alle kvantemekaniske beregninger av energinivå og bølgefunksjoner i realistiske potensial, er bruk av den tidsuavhengige Schrödinger-ligningen den foretrukne og i det hele tatt praktisk anvendelige fremgangsmåte. Men akkurat for den harmoniske oscillatoren er denne analytiske metoden den mest omstendelige. Det kan man se fra ligningen som i dette tilfelle blir
Den kan ikke uten videre løses ved kjente funksjoner. Men den kan forenkles ved å betrakte den først i store avstander fra origo.[4]
Ved å innføre den dimensjonsløse koordinaten
vil den opprinnelige differensialligningen omformes til
Når den variable x blir veldig stor, dominerer leddet med den potensielle energien på høyre side. Dette er et klassisk forbudt område og tilsvarer at impulsen til partikkelen er rent imaginær. Bølgefunksjonen vil avta raskt mot null her. Beholder man derfor bare dette leddet, vil ψ(x) = exp(-x2/2) være en approksimativ løsning i dette området.
Hvis man faktoriserer ut dette dominerende leddet i store avstander fra den eksakte bølgefunksjonen, kan denne skrives som
hvor H(x) er en ny funksjon som må bestemmes. Ved å sette inn denne formen på løsningen i den fulle ligningen, tar den formen
Dette er Hermites differensialligning. For at den skal ha løsninger som ikke dominerer over den eksponensielt avtagende oppførselen i store avstander, må parameteren λ være et oddetall. Skriver man derfor λ = 2n + 1 med n = 0, 1, 2 og så videre, finner man igjen de kvantiserte energinivåene
i overensstemmelse med hva man mer direkte fant med den algebraiske metoden.[4]
Flere dimensjoner rediger
Hamillton-operatoren for en harmonisk oscillator som kan svinge med samme frekvens i N forskjellige retninger, er
når den svingende massen er m = 1. Systemet kan derfor betraktes som bestående av N uavhengige 1-dimensjonale oscillatorer. Hver av dem kan derfor kvaanjiseres ved å innføre stigeoperatorene
og deres adjungerte. De vil da oppfylle de kanoniske kommutatorene
Uttrykt ved antallsoperatorene blir nå Hamilton-opertoren
hvorav energien til den multidimensjonale oscillatoren kan avleses direkte. Bortsett fra grunntilstanden med energi er alle andre energinivå degenererte da det er mer enn én kvantetilstand som har den samme energien.[3]
Todimensjonal oscillator rediger
Denne degenerasjonen er enklest å studere for N = 2 dimensjoner. Da kan man skrive Hamilton-operatoren som
Istedenfor stigeoperatorene og er det her hensiktsmessig å innføre de lineære kombinasjonene
De eneste kommutatorene som da er forskjellige fra null, blir
og utgjør derfor et nytt sett med stigeoperatorer. De inngår i Hamilton-operatoren på den nye formen
men deres fysiske innhold kommer først frem i operatoren for dreieimpulsen til oscillatoren. Denne vektoren står vinkelrett på xy-planet der bevegelsen foregår og kan nå skrives som
Antallsoperatoren angir derfor antall kvant med dreieimpuls +ħ, mens angir tallet på dem med -ħ. Hvert av disse kvantene har samme energi ħω.
Hvis n± er egenverdiene til disse to antallsoperatorene, er hvert energinivå til den todimensjonale oscillatoren gitt ved formelen
hvor er det totale antall kvant i dette nivået. Hvis hver kvantetilstand angis ved kvantetallene vil det nesten allltid være flere tilstander med samme energi. Det eneste unntaket er grunntilstanden (0, 0) som har laveste energi med n = 0. Første eksiterte energinivå med n = 1 består av D = 2 tilstander (1, 0) og (0, 1). mens det neste med n = 2 inneholder tilstandene (2, 0), (1, 1) og (0, 2). Generelt er degenerasjonen av nivå En gitt som D = n + 1.
SU(2) symmetri rediger
Kvantemekanisk degenerasjon skyldes vanligvis at systemet har en symmetri. For eksempel vil hvert energinivå for en partikkel i et sentralsymmetrisk potensial i tre dimensjoner, bestå av 2ℓ + 1 tilstander der kvantetallet ℓ = 0, 1, 2, ... angir størrelsen til den kvantiserte dreieimpulsen. Dette skyldes rotasjonssymmetrien til systemet.
Den todimensjonale oscillatoren har kun en rotasjonssymmetri om z-aksen som betyr at kommutatoren Men denne opplagte symmetrien er del av en større symmetri som kan tydeliggjøres ved de tre operatorene
Da hver av dem skaper et kvant samtidig som de fjerner et kvant, vil de ikke forandre energien til systemet og derfor kommutere med Hamilton-operatoren. I tillegg har de kommutatorene
seg i mellom. Vektoroperatoren med utgjør dermed en kvantisert dreieimpuls og genererer Lie-gruppen SU(2).
Hamilton-operatoren for oscillatoren er forbundet med kvadratet av denne operatoren med egenverdiene s(s + 1). Den nøyaktige sammenhengen er
slik at egenverdiene blir E = ħω(2s + 1) der spinnkvantetallet s = 0, 1/2, 1, 3/2 og så videre. Dette er i overenstemmelse med energinivåene En med n = 2s hvor også degenerasjonen D = 2s + 1 får en forklaring.[5]
For den generelle oscillatoren i N dimensjoner er det en tillsvarende degenerasjon av hvert energinivå En som skyldes symmetrigruppen SU(N). I tre dimensjoner gir den en degenerasjon som er D = (n + 1)(n + 2)/2 og er identisk med dimensjonen til de symmetriske representasjonene av symmetrigruppen SU(3).[3]
Bølgefunksjoner rediger
Stigeoperatorene for den todimensjonale oscillatoren kan også benyttes til å konstruere egenfunksjonene for de tilsvarende kvantetilstandene. Når operatorene uttrykkes ved den komplekse koordinaten z = √λ(x + iy) hvor λ = ω/ħ, tar de formen
Grunntilstanden inneholder ingen kvant slik at den tilsvarende bølgefunksjonen må oppfylle Dette kravet gir en førsteordens differensialligning med løsningen
Som forventet er den et produkt av bølgefunksjone for grunntilstandene til to éndimensjonale oscillatorer, henholdsvis i x- og i y-retning.
Ved å anvende heveoperatoren på denne funksjonen n ganger, fremkommer bølgefunksjonen
Den beskriver en tilstand med energi En = ħω(n + 1) og dreieimpuls Lz = nħ. Bølgefuksjoner med samme energi, men mindre dreieimpuls kan så finnes ved å anvende senkeoperatoren en tilstrekkelig antalll ganger på denne maksimale egenfunksjonen. De kan uttrykkes ved Laguerre-polynom som også opptrer i løsninger av Schrödinger-ligningen for hydrogenatomet i tre dimensjoner.
Referanser rediger
- ^ a b D.J. Griffiths, Quantum Mechanics, Pearson Education International, Essex (2005). ISBN 1-292-02408-9.
- ^ H. Kragh, Preludes to dark energy: Zero-point energy and vacuum speculations, arXiv:1111.4623.
- ^ a b c d R. Shankar, Principles of Quantum Mechanics, Plenum Press, New York (1982). ISBN 0-306-40397-8.
- ^ a b R.L. Liboff, Introductory Quantum Mechanics, Pearson Education, New Jersey (2003). ISBN 0-8053-8714-5.
- ^ E.S. Abers, Quantum Mechanics, Pearson Education, New Jersey (2004). ISBN 0-13-146100-1.
Eksterne lenker rediger
- HyperPhysics, Quantum Harmonic Oscillator