Oktonion

Oktonion (fra latin octo - åtte) eller Cayley-tall er et element i en åttedimensjonal utvidelse av de reelle tallene på samme måte som kvaternionene er en firedimensjonal utvidelse. Den tilsvarende tallmengden betegnes vanligvis med O eller $\mathbb {O}$ . Tallene kommuterer ikke ved multiplikasjon og denne operasjonen er heller ikke assosiativ. I motsetning til kvaternionene kan de derfor ikke representeres ved matriser og har ingen kjente, praktiske anvendelser. Innen ren matematikk knyttes de til spesielle Lie-grupper og deres egenskaper.

Tallmengdene R av reelle tall, C av komplekse tall, H av kvaternioner og O av oktonioner er de eneste divisjonsalgebraene over de reelle tallene som er normerte, det vil si at hvert element kan tilordnes en entydig, numerisk verdi.

Historie rediger

Dagen etter at William Rowan Hamilton i oktober 1843 oppdaget kvaternionene, skrev han om disse i et brev til sin venn John Thomas Graves. I desember samme år kunne Graves fortelle Hamilton at han hadde kommet frem til en lignende, åttedimensjonal utvidelse som han kalte for «oktaver». Komponentene oppfylte en «åtte-kvadraters identitet» av samme form som fire-kvadrats identiteten for komponentene til to kvarterioner.

På samme tid hadde også den unge Arthur Cayley fattet interesse for Hamiltons kvaternioner. I et publisert arbeid om elliptiske funksjoner i 1845 tok han med et appendiks hvor han presenterte egenskapene til dagens oktonioner som han hadde kommet frem til på egen hånd. Selv om Hamilton kunne bekrefte at Graves hadde gjort dette tidligere, ble det likevel arbeidet til Cayley som ble lagt merke til. Disse nye tallene fikk dermed Cayleys navn knyttet til seg.^[1]

I tillegg viste det seg at åtte-kvadraters identiteten til Graves var tidligere funnet i en annen sammenheng av Carl F. Degen som hadde hjulpet Niels H. Abel da han ennå var student.^[2]

Definisjon rediger

Oktonioner er element i et åttedimensjonalt vektorrom med basisvektorer 1, e₁, e₂, e₃, e₄, e₅, e₆ og e₇ slik at de kan skrives som

x=x_{0}+x_{1}\mathbf {e} _{1}+x_{2}\mathbf {e} _{2}+x_{3}\mathbf {e} _{3}+x_{4}\mathbf {e} _{4}+x_{5}\mathbf {e} _{5}+x_{6}\mathbf {e} _{6}+x_{7}\mathbf {e} _{7}

hvor de åtte komponentene (x₀,x₁,x₂,x₃,x₄,x₅,x₆,x₇) er reelle tall. De første komponenten x₀ sies å tilhøre den skalare delen av oktonionen, mens de syv andre tilhører den vektorielle eller «imaginære» delen.

Basiselementene danner en divisjonsalgebra slik at produktet av to element alltid kan uttrykkes som en lineærkombinasjon av dem selv. To oktononioner x og y kan derfor multipliseres sammen med resultat xy eller yx som også er oktonioner. I allminnelighet er xy ≠ yx slik at de i allminnelighet ikke kommuterer med hverandre.

Hvert element x skal også ha en bestemt norm |x | slik at |xy | = |x | |y |. Den kan beregnes fra den konjugerte x* av hver oktonion, definert

x^{*}=x_{0}-x_{1}\mathbf {e} _{1}-x_{2}\mathbf {e} _{2}-x_{3}\mathbf {e} _{3}-x_{4}\mathbf {e} _{4}-x_{5}\mathbf {e} _{5}-x_{6}\mathbf {e} _{6}-x_{7}\mathbf {e} _{7}

hvor produktet må være slik at

x^{*}x=x_{0}^{2}+x_{1}^{2}+x_{2}^{2}+x_{3}^{2}+x_{4}^{2}+x_{5}^{2}+x_{6}^{2}+x_{7}^{2}

Da kan den inverse x^-1 til oktonion x finnes som

x^{-1}={x^{*} \over |x|^{2}}

slik at den oppfyller betingelsen x x^-1 = x^-1x = 1. Graves og Cayley viste at produkter mellom de forskjellige basiselementene kan finnes slik at disse egenskapene ved oktonionene er oppfylt.^[1]

Cayley-Dicksons konstruksjon rediger

	1	e₁	e₂	e₃	e₄	e₅	e₆	e₇
1	1	e₁	e₂	e₃	e₄	e₅	e₆	e₇
e₁	e₁	−1	e₃	-e₂	e₅	-e₄	-e₇	e₆
e₂	e₂	−e₃	−1	e₁	e₆	e₇	-e₄	-e₅
e₃	e₃	e₂	−e₁	−1	e₇	-e₆	e₅	-e₄
e₄	e₄	-e₅	−e₆	−e₇	−1	e₁	e₂	e₃
e₅	e₅	e₄	-e₇	e₆	−e₁	−1	-e₃	e₂
e₆	e₆	e₇	e₄	-e₅	−e₂	e₃	−1	-e₁
e₇	e₇	-e₆	e₅	e₄	-e₃	−e₂	e₁	−1

Den enkleste og meste brukte fremgangsmåte for å finne multiplikasjonsregler mellom basiselementene som tilfredsstiller disse betingelsene, går tilbake til det første arbeidet til Cayley^[3] som senere ble videreført av Dickson.^[4]

På samme måte som kvaternioner kan defineres som et par av komplekse tall, kan man tenke seg oktonioner som bestående av et tallpar (P,Q ) der P og Q er kvaternioner. Det tilsvarer å utvide vektorrommet for disse som er gitt ved basiselementene 1, i, j og k med et nytt, imaginært basiselement e. En oktonion kan dermed skrives som

{\begin{aligned}x&=(P,Q)=P+Q\mathbf {e} \\&=p_{0}+p_{1}\mathbf {i} +p_{2}\mathbf {j} +p_{3}\mathbf {k} +(q_{0}+q_{1}\mathbf {i} +q_{2}\mathbf {j} +q_{3}\mathbf {k} )\mathbf {e} \end{aligned}}

der e e = e² = -1. De syv vektorielle basiselementene for oktonionene er dermed e₁ = i, e₂ = j, e₃ = k, e₄ = e, e₅ = i e, e₆ = j e og e₇ = k e. Disse kan multipliseres sammen basert på en generalisering av produktregelen for kvaternioner. Den gir

{\begin{aligned}(P_{1},Q_{1})(P_{2},Q_{2})&=(P_{1}+Q_{1}\mathbf {e} )(P_{2}+Q_{2}\mathbf {e} )\\&=P_{1}P_{2}-Q_{2}^{*}Q_{1}+(Q_{2}P_{1}+Q_{1}P_{2}^{*})\mathbf {e} \end{aligned}}

hvor rekkefølgen av faktorene i produktene er viktig da kvaternionene ikke kommuterer med hverandre. Med denne notasjonen er den konjugerte av oktonion x = P + Q e gitt som

x^{*}=P^{*}-Q\mathbf {e}

slik at produktregelen gir den ønskede normen x*x = P *P + Q *Q. Samme regel gir også som forventet at e₅ e₅ = (i e)(i e) = -i*i = i² = - 1 og likedan e₆ e₆ = e₇ e₇ = -1. Alle produktene kan samles i en kvadratisk tabell hvor elementene er plassert antisymmetrisk om diagonalen med negative enere.^[2]

En konsekvens av disse regnereglene er at multiplikasjon ikke er assosiativ. For eksempel kan man fra tabellen se at e₄(e₅ e₆) = e₇, mens (e₄ e₅)e₆ = -e₇. For tre vilkårlige oktonioner x, y og z gjelder derfor ikke lenger at x(y z) kan settes lik med (x y)z. Derimot har man generelt de mer spesielle egenskapene

x(xy)=(xx)y,\;\;\;x(yy)=(xy)y,

som uttrykker en form for «alternativitet».^[2]

Fano-planet rediger

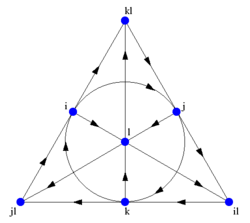
De vektorielle basiselementene utgjør de syv punktene i Fano-planet. Multiplikasjon av oktonioner følger fra de tre punktene på hver av de syv linjene i planet.

Produktene av de vektorielle basiselementene som følger fra konstruksjonen til Cayley og Dickson, kan også elegant gjengis i Fano-planet. Det består av syv punkter knyttet sammen ved syv linjer bestående av tre punkt abc. Hvis punktene angis som vist i figuren, er de tilsvarende linjene 123, 145, 176, 246, 257, 347, 365. Hver linje har en syklisk retning slik at produktet av to basisvektorer

\mathbf {e} _{a}\mathbf {e} _{b}=\mathbf {e} _{c}=-\mathbf {e} _{b}\mathbf {e} _{a}

når indeksene abc følger denne retningen. For eksempel inkluderer dette den fundamentale sammenhengen e₁ e₂ = e₃, men også e₂ e₄ = e₆ og e₃ e₄ = e₇.

Det er forbindelsen til Fano-planet som i stor grad forbinder oktonionene med egenskaper til noen av de mest spesielle Lie-gruppene.

Se også rediger

Referanser rediger

^ ^a ^b J.H. Conway and D.A. Smith, On Quaternions and Octonions: Their Geometry, Arithmetic, and Symmetry, CRC Press, Boca Raton (2003). ISBN 978-1-56881-134-5.
^ ^a ^b ^c J.C. Baez, The Octonions, Bull. Amer. Math. Soc. 39, 145-205 (2002). arXiv:math/0105155
^ A. Cayley, On certain Results relating to Quaternions, Philosophical Magazine 26(3), 141-145 (1845).
^ L.E. Dickson, On Quaternions and Their Generalization and the History of the Eight Square Theorem, Annals of Mathematics, 20(3), 155–171 (1919).

Eksterne lenker rediger

J.C. Baez, Octonions, informative websider
Quanta Magazine, Octonions in particle physics?

[Conway-1] J.H. Conway and D.A. Smith, On Quaternions and Octonions: Their Geometry, Arithmetic, and Symmetry, CRC Press, Boca Raton (2003). ISBN 978-1-56881-134-5.

[Baez-2] J.C. Baez, The Octonions, Bull. Amer. Math. Soc. 39, 145-205 (2002). arXiv:math/0105155

[Cayley-3] A. Cayley, On certain Results relating to Quaternions, Philosophical Magazine 26(3), 141-145 (1845).

[Dickson-4] L.E. Dickson, On Quaternions and Their Generalization and the History of the Eight Square Theorem, Annals of Mathematics, 20(3), 155–171 (1919).

[1]

[2]

[3]

[4]