Kapasitans
Kapasitans til en elektrisk leder sier hvor mye elektrisk ladning Q den kan ta opp når den pålegges en viss elektrisk spenning V i forhold til omgivelsene. Lederen kalles i dette tilfellet for en kapasitet eller kondensator. Dens kapasitans betegnes vanligvis ved bokstaven C og er definert ved sammenhengen
Ved bruk av SI-systemet måles den i enheter av Farad hvor 1 F = 1 Coulomb/1 Volt. Dens størrelse avhenger av lederens geometriske form og hva slags materiale den befinner seg i.
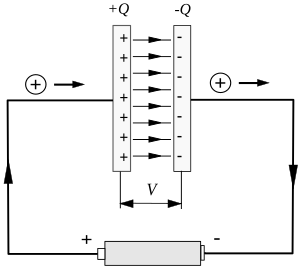
Den mest kjente kapasitet består av to parallelle, metalliske plater som har mye større utstrekning enn deres gjensidige avstand. Ladningen Q er da like stor og med motsatt fortegn på hver plate, mens spenningen V er forskjellen i elektrisk potensial mellom dem. Dette er en videreutvikling og forenkling av Leidnerflasken som ble brukt til å lagre elektrisk ladning i begynnelsen av forrige århundre. Den kan ha en kapasitans av størrelsesorden μF eller microfarad. I moderne elektronikk benyttes kondensatorer som har en utstrekning som er mye mindre enn mikrometer og nærmer seg størelsen til enkelte atomer. Deres kapasitans varierer fra noen pF eller picofarad til enda mindre verdier.
Kondensatorer rediger
En platekondensator består av to parallelle, metalliske plater med gjensidig avstand d. Når den er mye mindre enn utstrekningen til platene, kan det elektriske feltet E mellom dem betraktes som tilnærmet konstant. Når hver plate har arealet A, kan det beregnes ved bruk av Gauss' lov som gir
når det er luft mellom platene med dielektrisitetskonstant som kan settes lik ε0 i SI-systemet. Den elektriske spenningen mellom dem er V = Ed som betyr at kapasitansen for platekondensatoren er
Vanligvis lages denne ved å ha et isolerende materiale med en dielektrisitetskonstant ε > ε0 mellom platene slik at kapasitansen blir tilsvarende større.[1]
En sfærisk kondensator består av to konsentresiske kuleskall med radius henholdsvis R1 og R2. Hvert av disse bærer en ladning ±Q. Det elektriske spenningen mellom dem er da
når materialet mellom dem har dielektrisitetskonstant ε. Herav kan kapasistansen for denne kondensatoren avleses. Når R2 blir veldig stor, finner man kapasitansen C = 4π εR1 for et enkelt kuleskall. På samme måte kan den beregnes også for noen andre, enkle geometrier.[2] Resultatene kan sammenfattes i tabellen:
| Type kondensator | Kapasitans | Geometri |
|---|---|---|
| parallelle plater | ||
| koaksiale sylindrer | ||
| konsentriske sfærer | ||
| kuleskall | ||
| parallelle sylindrer |
Elektrisk feltenergi rediger
De to platene med motsatte ladninger i en platekondensator trekkes mot hverandre av elektriske krefter og må mekanisk holdes på plass. Kondensatoren inneholder derfor energi som er lagret i det elektriske feltet. Denne oppsto under oppladningen hvor man gradvis overfører små ladninger dq fra den ene platen til den andre. Under denne prosessen vil ladningen q på hver plate variere fra 0 til Q, noe som gir en tilsvarende, variabel spenning q /C mellom platene. Det totale arbeidet som utføres under oppladningen, er dermed
Denne energien er lagret i det elektriske feltet mellom platene og kan skrives som
der Ad er volumet av rommet mellom platene. Dette er i overensstemmelse med det generelle uttrykket for den elektriske feltenergien i elektrostatikken.[3]
Man kan på samme vis betrakte flere, isolerte ledere som hver har et elektrisk potensial Vi og bærer en elektrisk ladning Qi. Dette systemet av ladninger vil da ha en elektrostatisk energi
hvor Ci = Qi /Vi er kapasitansen til den i-te lederen.
Serie og parallellkobling rediger
Ved en seriekobling av kondensatorene C1, C2 og Cn kobles de etter hverandre til en ytre spenningskilde V. Det vil da skapes ladninger ±Q som er like store på hver kondensator. Det betyr at spenningen over den i-te kondensatoren er Vi = Q /Ci. Den totale spennningen over alle kondensatorene er da summen
Dette kan skrives som V = Q /C hvor
gir den totale kapasistansen C av de seriekoblede kondensatorene. Den er mindre enn den minste av kapasitetene i serien. Hvis to like store kondensatorer kobles i serie, blir den resulterende kapasitansen halvert.[1]
Den motsatte effekten oppnås ved å koble kondensatorene parallelt med hverandre. Hver av dem er da utsatt for den samme spenningen V. Men i dette tilfelle vil det skapes forskjellige ladninger Qi = CiV på hver av dem. Den totale ladningen Q på alle kondensatorene er summen av disse og kan skrives som Q = CV hvor
er kapasitansen for de parallelkoblede kondensatorene. Ved å koble to like kondensatorer på denne måten, dobles derfor den resulterende kapasitansen.
RC-kretser rediger
Når man lader opp en kondensator med kapasitans C, vil spenningen over den VC = V og dens ladning Q = CV variere med tiden t. Dette kan i praksis gjøres ved å koble den til med ledninger en ytre spenningskilde Vin. Ledningen vil ha en viss, indre motstand R. Strømmen i denne seriekoblete kretsen er nå
hvor den går gjennom kondensatoren som en forskyvningsstrøm. Den gir samtidig et spenningsfall over motstanden som er RI. Kirchhoffs spenningslov gir da
Hvis den ytre spenningen Vin skrus på med full styrke V0 ved tiden t = 0, vil dermed spenningen over kondensatoren variere som
Den øker i begynnelsen raskt fra V = 0. Først etter en tid gitt ved tidskonstanten τ = RC, begynner den å nærme seg den påtrykte spenningen V0. Den samme tidskonstanten opptrer på en tilsvarende måte når en oppladet kondensator utlades gjennom en motstand.[3]
Vekselstrøm rediger
Når den påtrykte spenning er en vekselstrøm med vinkelfrekvens ω = 2π f, opptrer kapasitansen C som en nye type elektrisk motstand. Den kalles kapasitiv reaktans og har størrelse
En ren likestrøm kan ikke gå gjennom en kondensator, noe som tilsvarer at XC → ∞ når ω → 0.
Ladningen Q på kondensatoren varierer nå med samme frekvens slik at man kan skrive Q(t ) = Q0 sinωt. Spenningen over den er dermed
Den bestemmer strømmen i kretsen som derfor blir I = dQ/dt = Q0 ω cosωt. Når den går gjennom den seriekoblede motstanden, gir den samtidig spenningsfallet
Spenningene over motstanden og kapasitansen er derfor faseforskjøvet med 90° i forhold til hverandre. Det betyr igjen at strømmen i kretsen vil være faseforskjøvet i forhold til den påtrykte vekselspenningen.[1] Disse forholdene kan enklest beskrives ved bruk at fasevektorer for de forskjellige strømmene og spenningene i en slik krets.
Referanser rediger
- ^ a b c F. Bugge, Lærebok i Radio, Aschehoug & Co., Oslo (1940).
- ^ G.L. Pollack and D.R. Stump, Electromagnetism, Addison-Wesley, San Fransisco (2002). ISBN 0-8053-8567-3.
- ^ a b O. Hunderi, J.R. Lien og G. Løvhøiden, Generell fysikk for universiteter og høgskoler, Bind 2, Universitetsforlaget, Oslo (2001). ISBN 978-82-1500-006-0.
Eksterne lenker rediger
- Physics LibreTexts, Capacitors and Dielectrics, online pedagogisk fremstilling
