Prisme (optikk)
Et prisme i optikken er et transparent materiale med flate sider. Den mest kjente formen har tre sider og kan brukes til å dele opp hvitt lys i ulike farger. Andre former brukes til å reflektere lyset for eksempel i kikkerter eller for å polarisere lys.
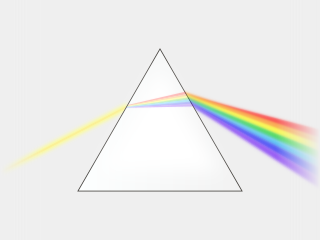
Når lys går gjennom en grenseflate mellom to stoff med ulik brytningsindeks, vil det forandre retning ved at det brytes på en måte som er bestemt av Snells brytningslov. Avbøyningen i et prisme vil avhenge av brytningsindeksen til materialet det er laget av. På grunn av dispersjon er denne avhengig av bølgelengden til lyset. Da hvitt lys inneholder ulike bølgelengder, vil dette bli splittet opp i forskjellige farger tilsvarende disse bølgelengdene.
Lys som beveger seg ut av prismet, vil passere en grenseflate mot luft som har en mindre brytningsindeks enn materialet i prismet. Hvis innfallsvinkelen ved denne flaten er tilstrekkelig stor, vil lyset totalreflekteres. Det er denne effekten som blir benyttet i mange kikkerter.
Ved hver gjenomgang av lyset mellom to stoff med ulik optisk tetthet, vil en del av lyset brytes mens resten reflekteres tilbake. Hvor stor del av det innkommende lyset som går over i disse to komponentene, er bestemt av Fresnels formler. Hver komponent vil også ha forskjellig polarisering. Kombineres denne effekten med totalrefleksjon i en slik grenseflate, kan man skape polarisert lys som i et Nicol-prisme.
Dispersjon rediger
I et transparent eller gjennomsiktig materiale absorberes ikke noe lys i den synlige delen av det elektromagnetiske spektret. Materialet er holdt sammen ved sterke bånd som først påvirkes av mer energetisk lys som tilsvarer kortere bølgelengder i den ultrafiolette delen av spektret. Av samme grunn vil også brytningsindeksen til lyset påvirkes mest i dette område og derfor avta for økende bølgelengder. Dette kalles for normal dispersjon.[1]
Denne sammenhengen ble først uttrykt ved Cauchys formel for brytningsindeksen n. Kalles bølgelengden for λ, kan den i sin enkleste utgave skrives som
hvor A og B er konstanter som karakteriserer hvert materiale. Fra moderne atomfysikk kan disse nå beregnes ved bruk av kvantemekanikk.[2]
Ved normal dispersjon er begge disse konstantene positive og blått lys vil ble avbøydd mer enn rødt ved gjennomgang i et glassprisme. Det røde lyset blir derfor liggende over det blå. Av lignende grunn er denne rekkefølgen av fargene den samme som i regnbuen.[3]
Avbøyningsvinkel i trekantprisme rediger
Når lys av en viss bølgelengde går gjennom et prisme med en likebeint trekant som grunnflate, kan dets avbøyningsvinkel beregnes enklest når det går vinkelrett gjennom en av sideflatene og ut en annen. Kalles den første innfallsvinkelen α1, er den brutte vinkelen β1 gitt ved Snells brytningslov
der n er brytningsindeksen til materialet i prismet. For luften omkring antas n = 1. På samme måte har man
for siden der lyset kommer ut av prismet. Den totale avbøyningsvinkelen er nå δ = (α1 - β1) + (α2 - β2) som forenkles til
når man benytter at β1 + β2 = ω som er toppvinkelen i den likebeinte trekanten.[3]
Avbøyningsvinkelen δ varierer med innfallsvinkelen α1 og kan finnes fra
Den vil ha en minimum δm når lysstrålen går gjennom prismet parallelt med grunnlinjen i trekanten. Dette følger fra symmetrien i problemet.[1] Da er α1 = α2 = α slik at
I tillegg vil man i dette spesielle tilfellet ha β1 = β2 = ω/2 slik at Snells lov i de to grenseflatene gir
Da vinkelen ω er kjent, vil en måling av den minimale avbøyningsvinkelen dermed kunne gi en meget nøyaktig bestemmelse av brytningsindeksen for dette materialet ved denne bølgelengden.[4]
Referanser rediger
- ^ a b F.A. Jenkins and H.E. White, Fundamental of Optics, McGraw-Hill, New York (2001). ISBN 0-07-256191-2.
- ^ W. Demtröder, Electrodynamics and Optics, Springer, New York (2019). ISBN 978-3-0300-2289-1.
- ^ a b R.W. Wood, Physical Optics, Dover Publications, New York (1967).
- ^ E. Hecht, Optics, Addison-Wesley, Reading, Massachusetts (1998). ISBN 0-201-30425-2.