Pol (elektronikk)
Med en enkelt pol menes her en knekk i frekvensresponsen i en analog signal-overføringskjede[trenger referanse] der forskjellen i stigning over og under pol-frekvensen er 6.02 dB per oktav (= 20.00 dB per dekade). Polene utføres som spenningsdelere bestående av en resistans og en reaktans.



Poler utgjør atomene eller byggeklossene til de mere omfattende generelle elektroniske filtre.[trenger referanse]
Enkle poler kan i analog elektronikk kun dannes ved kombinasjon av resistanser R og reaktanser som kapasitanser C og induktanser L. Denne artikkelen ser nøyere på R-C og R-L kombinasjonene som danner enkle poler, men tar ikke for seg L-C(-R)-kombinasjoner, som av natur er topolte.
Enkelt pol rediger
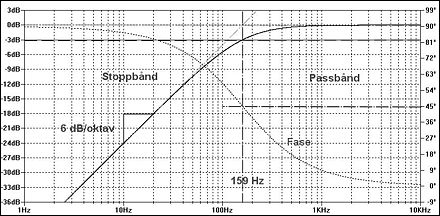
En enkelt pol kan være konfigurert som et lavpass- (LPF) eller som et høypassfilter (HPF). Til høyre ses frekvens- og faseresponsene for et lavpassfilter øverst, figur 1, og for et høypassfilter under, figur 2.
- Et høypassfilter har en frekvensrespons som stiger ved lave frekvenser og er flat for høye. Faseresponsen er +90 grader for svært lave og 0 grader for svært høye frekvenser. For polfrekvensen er fasen 45 grader.
- Et lavpassfilter har en frekvensrespons som er flat ved lave frekvenser og avtar for høye. Faseresponsen er 0 grader for svært lave og -90 grader for svært høye frekvenser. For polfrekvensen er fasen -45 grader. Se figurene 1 og 2.
En enkelt pol kan dannes på to måter:
- Med en motstand og en kondensator (kapasitans) (RC)
- Med en motstand og en spole (induktans) (RL)
Hvert av disse parene kan kobles som et HPF eller som et LPF. Figur 3 illustrerer dette.
Hver enkelt pol karakteriseres av sin knekk- eller polfrekvens. Frekvensen finnes der reaktansen for kondensatoren eller spolen har samme absoluttverdi som motstanden har. Polfrekvensene blir:
- For RC : f = 1 /(2*π*R*C)
- For RL : f = R /(2*π*L)
Ved polfrekvensen ligger frekvensresponsen 3.01 dB lavere enn den flate delen og faseresponsen er +45 (HPF) eller -45 (LPF) grader. Der frekvensresponsen stiger mot høye frekvenser er fasen alltid positiv; den er 0 der det er flatt og negativ der den synker. Figur 4 illustrerer inngangsspenningen (rød) og utgangsspenningene ved polfrekvensen for et LPF og et HPF. Positiv fase betyr at bølgen ligger før inngangsbølgen, altså til venstre i tidsdiagrammet. Til venstre ses innsvingningsforløpet etter at generatoren ble koplet til ved t = 0 ms.
Frekvensområdet for den flate delen av responsen kalles passbåndet, den andre delen kalles stoppbåndet. Betegnelsene LPF og HPF sier om passbåndet ligger ved lave eller ved høye frekvenser.
De angitte tallverdier og egenskaper gjelder for alle enkle poler. Responsene er fullstendig definert ved "énpolt LPF" eller "énpolt HPF", samt polfrekvensen. Byggemåten kan i tillegg angis med "RC" eller "RL".
For illustrasjonene er det brukt en motstandsverdi med verdien 1 kΩ, en kondensator med verdien 1 μF og en spole med verdien 1 H, der kombinasjonen gir en polfrekvens ved 159.155 Hz for begge filtertypene.
Produktet R*C eller forholdet R/L bestemmer polfrekvensen. For RC kan en øke R og minke C tilsvarende, eller en kan for RL øke eller minke (multiplikativt) verdiene like mye uten at frekvensen flyttes. Det kunne altså vært brukt 1 MΩ og 1 nF eller 1 MΩ og 1000 H som komponentverdier til illustrasjonene uten at noe hadde endret seg i figurene. Endringer medfører endringer i polens impedans, som igjen beskriver hva som kreves av kilden (dens utgangsimpedans) og av den etterfølgende lasten (neste trinns inngangsimpedans).
- Ekstreme frekvenser
- Figurene 5 og 6 søker å illustrere både funksjonsprinsipper og impedansforhold ved ekstreme frekvenser. Ved svært høye frekvenser (relativt til polfrekvensen) blir kondensatorer erstattet av ledere, og spoler forsvinner. Ved svært lave frekvenser blir spoler erstattet av ledere, og kondensatorer forsvinner.
- Hvert resulterende enkeltdiagram finnes i begge figurene.
Matematisk rediger
Med RC-kombinasjonen som eksempel blir:
Spenningen over C i forhold til inngangsspenningen (Gain C, LPF ut))
og spenningen over R i forhold til inngangsspenningen (Gain R, HPF ut)
- ,
og fasevinklene blir:
for C (LPF fase)
og for R (HPF fase)
- .
For polfrekvensen eller knekkpunktet er betingelsen
oppfylt. Der er fasevinkelen -45 grader og GC og GR begge lik i absoluttverdi.
Kombinasjonen av C og L (med eller uten R i tillegg) danner et topolt filter som oppfører seg vesentlig forskjellig fra enkle poler, særlig fordi det oppstår et resonansfenomen. L og C sine reaktanser har da motsatte fortegn og dersom absoluttverdiene er like kan de kansellere hverandre til null eller bli usynlige til uendelig impedans, ideelt sett. Beskrivelse av slike filtre er langt mere komplisert enn RC og RL-kombinasjoner og ligger utenfor rammen til denne artikkelen.
Komponent-kombinasjonene som danner en pol utgjør den fundamentale byggeklossen for de fleste ikke-LC filtre. RC-kombinasjonen er alltid brukt hvis det ikke er en spesiell grunn til å bruke RL. Spoler er vanligvis dyrere, finnes i færre verdier, er fysikalsk større og tyngre og har høyere effekttap enn C.
- Begrepet pol stammer fra inntrykket som en teltstav (eng. "pole" = påle) gjør på en teltduk, sett utenfra teltet[trenger referanse]. Ordbruken innen elektronikk henger sammen med bruken av begrepet "pol" i matematisk sammenheng.
Sammensatte poler rediger
Flere poler kan settes sammen for å skape en ønsket frekvens- eller faserespons. Selv om muligheten er svært mange er det ikke mulig å skape en hvilken som helst tenkelig respons. Hvor rammene for det mulige settes beskrives av allmenn filterteori.
Gjensidig belastning rediger
Når to poler koples etter hverandre vil den siste belaste den første. Det fører til at den resulterende responsen ikke blir helt lik den ideelle virkningen gitt av to enkeltstående poler. Dette kan, men må ikke, være en uønsket effekt.
- For å avmilde problemet kan det brukes et høyere impedansnivå i det andre filtret enn i det første.
- For å fjerne problemet kan det brukes +1x spenningsforsterkere (som har høy inn- og lav utgangsimpedans) etter hver enkelt pol. Dette krever strømforsyning og elektronikk, og introduserer litt støy til signalet.
- Når den ene polen er RC- og den andre er RL-basert kan det komme til en resonans mellom L og C som endrer responsene vesentlig i forhold til to samme-type kombinasjoner.
Båndpass rediger
Settes et LPF etter et HPF eller omvendt, og de har (frekvens-)overlappende passbånd, dannes et båndpassfilter (BPF). Frekvensene i passbåndet passerer filterkombinasjonen, mens både høye og lave frekvenser svekkes. Har filtrene samme polfrekvens blir passbåndet redusert til et maksimumspunkt i frekvensresponsen.
Båndstopp rediger
Et båndstoppfilter demper signalet i et visst frekvensbånd, mens lave og høye frekvenser passerer. Et passivt båndstoppfilter kan ikke realiseres med to etterfølgende enpolte filtre, siden frekvensandelene til det andre filtret allerede er fjernet i det første. De to filtrene må begge få inngangsspenningen og utgangsspenningene må adderes, noe som krever bruk av forsterkerkoplinger.
Flere like poler rediger
N poler av samme type (LPF eller HPF) og med samme polfrekvens koplet etter hverandre danner et filter som får steilere avsvekking i stoppbåndet. Stoppbåndet stiger eller synker med N*6.02 dB per oktav. Ideelt sett (uten gjensidig belastning) er responsen ved polfrekvensen N*(-3.01) dB. For mange filtre kan elektroniske buffere (+1x forsterkere) bli nødvendige mellom noen trinn, eller de koples som Sallen-Key-filtre (neste avsnitt).
Sallen-Key-filter rediger
Når to like poler kobles sammen blir kneet ved polfrekvensen ofte rundere enn ønsket. Et Sallen-Key-filter er et aktivt (forsterkende) topolt filter som kan gjøre knekken skarpere. Dette oppnås ved tilbakekopling fra en +1x forsterker. Koplingen er svært enkel og ble introdusert av R. P. Sallen og E. L. Key ved Massachusetts Institute of Technology-universitetet i USA i 1955. Ved innføring av noe forsterkning kan filtret til og med få en forsterkende topp ved den duale polfrekvensen, kjent som peak eller resonans.
Med 1x forsterkning i operasjonsforsterkeren oppstår den skarpeste knekken, akkurat uten noen topp, når impedansforholdet R1/R2 er , som er ca 0.414. C2/C1 må ha det samme forholdet. Dempingen er da bare 3 dB ved knekkfrekvensen. Når forholdet R1/R2 går mot 0, vil det oppstå en liten topp på noe over 1 dB ved knekkfrekvens og ved knekkfrekvensen er dempingen 0 dB. En topolet RC eller RL konfigurasjon, der polene ikke belaster hverandre, vil ha 6 dB dempning ved knekkfrekvensen. En passiv LC kombinasjon, dempet med en R = * X (spolen og kondensatorens X-verdi ved knekkfrekvensen), vil også ha 3 dB dempning ved knekkfrekvensen, frekvensresponsene er identiske. Se figur 8.
Høyere ordens LPF- og HPF-filtre rediger
Det er ofte ønskelig, i enkelte tilfeller nødvendig, å oppnå et LPF eller HPF som har en steil overgang mellom pass- og stoppbånd. Antall poler blir da noenlunde stort og R-L-C-kombinasjoner blir nødvendige. Denne problematikken er en vesentlig del av filterteorien, som er svært matematisk av natur. Opp til en viss grense kan slike filtre skapes uten at nye konsepter innføres. (Gausiske, Bessel- Butterworth filtre). For en enda steilere overgang (i Chebyshev- eller såkalte Elliptiske eller Cauer filtre) må passbåndet gjøres noe ruglete eller bølgete og stoppbåndet vil oppvise en viss signal-gjennomgang.