Pascals snegle

Pascals snegle eller limaçon er en plan kurve av fjerde grad. Den er en epitrokoide hvor forholdet mellom radiene til de to sirklene er R/r = 1. Ved bruk av polarkoordinater (r,θ) er den gitt ved ligningen

Pascals snegle for b/a > 1 og b/a < 1. Når b/a = 1, er den en kardioide.

$r(\theta )=a+b\cos \theta$

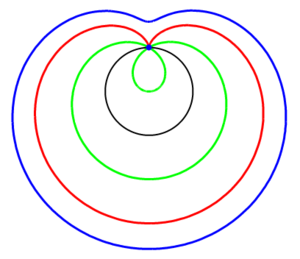
Dens form avhenger av forholdet b/a. I det spesielle tilfellet at b/a = 1, blir den en kardioide eller hjertekurve. Når a < b vil den skjære seg selv i et punkt slik at den inneholder en løkke. Derimot når a > 2b er den overalt konveks.

Kurven ble opprinnelig studert av Albrecht Dürer i sitt verk Underweysung der Messung fra 1525. Her ga han flere, geometriske metoder for å fremstille den. Omtrent hundre år senere ble dette arbeidet tatt opp igjen av Étienne Pascal som var far til Blaise Pascal. Siden er hans navn blitt knyttet til denne kurven.

Matematisk fremstilling

En limaçon kan fremstilles som en epitrokoide som består av to sirkler med samme størrelse.

Fra definisjonen kan kurven fremstilles i kartesiske koordinater ved sammenhengene x = r cosθ og y = r sinθ. De gir

$x(\theta )=a\cos \theta +{b \over 2}\cos 2\theta +{b \over 2}$

$y(\theta )=a\sin \theta +{b \over 2}\sin 2\theta$

Pascals sneglekurve er derfor en epitrokoide hvor argumentene til de trigonometriske funksjonene viser at den er generert av to sirkler med like store radier hvorav den ene ruller utenpå den andre. Konstanten b/2 tilsvarer en forflytning med den størrelse langs x-aksen.

En mer kompakt fremstilling av kurven fås ved bruk av den komplekse koordinaten z = x + iy. Den blir

$z=ae^{i\theta }+{b \over 2}e^{2i\theta }+{b \over 2}$

ved å benytte Eulers formel $e^{i\theta }=\cos \theta +i\sin \theta$. Hvis vinkelen θ øker jevnt med tiden t slik at θ = ωt der ω er vinkelhastigheten, beskriver de to eksponentialfunksjonene rotasjonen av den ene sirkelen hvis senter roterer utenfor den andre.

Fjerdegradskurve

En implisitt ligning for Pascals sneglekurve i kartesiske koordinater kan også gis. Den finnes mest direkte ved å skrive $r^{2}-bx=r(r-b\cos \theta )=ar$ slik at

$(x^{2}+y^{2}-bx)^{2}=a^{2}(x^{2}+y^{2})$

siden man har $r^{2}=x^{2}+y^{2}$. Denne kurven er derfor av fjerde grad.

Limaçon som omhyllingskurve

Pascals snegle kan fremstilles som omhyllingskurven for alle sirkler som har sitt senter på en gitt sirkel og går gjennom et gitt punkt. Hvis den gitte sirkelen har radius a og senter i punkt (b, 0) på x-aksen, kan man velge det gitte punkt å ligge i origo.

Et punkt på den gitte sirkelen har da koordinatene

$x_{c}=b+a\cos \theta \,,\;\;y_{c}=a\sin \theta$

hvor θ er en polar vinkel. Den kvadrerte radius til ny sirkel sentrert i dette punktet og som går gjennom origo, vil nå være

$r_{c}^{2}=x_{c}^{2}+y_{c}^{2}=a^{2}+b^{2}+2ab\cos \theta$

i overensstemmelse med cosinussetningen. Skaren av slike sirkler er gitt ved ligningen $(x-x_{c})^{2}+(y-y_{c})^{2}=r_{c}^{2}$ eller $F(x,y,\theta )=0$ hvor

$F(x,y,\theta )=x^{2}+y^{2}-2x(b+a\cos \theta )-2ya\sin \theta$

For at to sirkler i denne skaren med nesten samme verdi av parameteren θ skal tangere den samme omhyllingskurven, må F_θ = ∂F/∂θ = 0. Nå er F_θ = 2a(x sinθ - y cosθ) slik at denne betingelsen er oppfylt når punktene (x,y) på omhyllingskurven kan skrives på formen x = r cosθ og y = r sinθ. Den ukjente størrelsen r  bestemmes fra F = 0 som gir den ikke-trivielle løsningen r = 2(a + b cosθ). Bortsett fra en faktor 2, er dette ligningen for Pascals snegle.

Eksterne lenker

• MacTutor, Limaçon of Pascal, University of St. Andrews, Scotland.
• Albrecht Dürer, Underweysung der Messung, Wikisource
• E. Weisstein, Limaçon, Wolfram MathWorld.