Elektrisk felt

Elektrisk felt (også kalt elektrisk feltstyrke) gir kraften som virker i hvert punkt i rommet på en elektrisk ladet partikkel som der befinner seg i ro. Det er et vektorfelt som skapes av andre elektriske ladninger ifølge Coulombs lov eller fra et magnetfelt som varierer med tiden og beskrevet ved Faradays induksjonslov.

Det elektriske feltet er vanligvis betegnet ved vektorsymbolet E. En ladning q som er i ro i dette feltet, vil bli påvirket av kraften F = q E. I SI-systemet er derfor enheten for elektrisk feltstyrke Newton per Coulomb N/C som er lik Volt per meter, V/m. Begrepet elektrisk felt ble først introdusert av Michael Faraday på midten av 1800-tallet.

Varierer det elektriske feltet med tiden, vil det generere Maxwells forskyvningsstrøm som igjen skaper et magnetisk felt. Dette samspillet omtales som et elektromagnetisk felt og er beskrevet av Maxwells ligninger som danner grunnlaget for elektromagnetisk teori. Spesiell relativitetsteori forener det elektriske og magnetiske vektorfeltet i Faradays felttensor. Lys og annen elektromagnetisk stråling er bølger av disse feltene. I kvantemekanikken erstattes denne klassiske beskrivelsen med kvanteelektrodynamikk.

Karakteristiske feltstyrker rediger

I dagliglivet er vi omgitt av spenninger med størrelser som typisk er mellom et par volt opp til noen hundre volt over avstander på noen meter. Derfor vil vi fra elektriske installasjoner omkring oss være utsatt for elektriske feltstyrker E = (0.1 - 100) V/m. Nær høyspentlinjer vil man kunne ha mer enn 1000 V/m = 1kV/m. Feltene foran gammeldagse fjernsynskjermer kunne være mye sterkere. Likedan er vi hele tiden bombardert med elektromagnetisk stråling fra radioer og mobiltelefoner. For at signalene skal være hørbare, må disse bølgene inneholde felltstyrker større enn 10^-5 V/m.

Fra Naturens side er vi i tillegg utsatt for et mer konstant elektrisk felt med omtrentlig størrelse 130 V/m nær Jorden på grunn av atmosfærisk elektrisitet. Men det er likevel lite i forhold til hva som kan oppstå som statisk elektrisitet ved triboelektriske effekter. Ved så høye feltstyrker som 10⁶ V/m kan man få elektrisk gjennomslag i luften når elektroner blir revet løs fra atomene. Det kan arte seg som gnister eller en lysbue.^[1]

Enda sterkere felt finnes inne i atomene. Elektronet i et hydrogen-atom beveger seg i det elektriske feltet fra et proton i en avstand som er gitt ved en Bohr-radius. Det gir typiske feltstyrker av størrelsesorden 10¹² V/m. Det er dette elektriske feltet som delvis er grunnen til finstrukturen til forskjellige spektrallinjer i atomenes emisjonsspekter.

Ved enda høyere feltstyrker vil partikler og deres antipartikler oppstå spontant fra vakuum.^[2] Julian Schwinger har vist ved bruk av kvanteelektrodynamikk at slik pardannelse av elektron-positronpar vil opptre for elektriske felt

E>E_{c}={\frac {m_{e}^{2}c^{3}}{e\hbar }}=1.3\times 10^{18}{\rm {V/m}}

Her er e elektronets ladning, m_e dets masse, c er lyshastigheten og ħ = h/2π er den reduserte Planck-konstanten. Dette fenomenet gir løsningen på Kleins paradoks.^[3] Men det er ikke kjent hvor så sterke felt vil kunne opptre. Tilnærmet så høye felt kan finnes på overflaten av de aller tyngste atomkjerner.

Elektrostatiske felt rediger

Elektriske feltvektorer for en positiv punktladning peker utover og avtar i størrelse med kvadratet til avstanden fra ladningen.

Når alle elektriske ladninger og strømmer i et system ikke forandrer seg med tiden, vil de resulterende feltene også være konstante eller «statiske». Alle elektriske felt kan da i utgangspunktet beregnes fra Coulombs lov som danner grunnlaget for elektrostatikken. Den sier at en ladning q i vakuum vil skape et elektrisk felt i et punkt r = (x,y,z) som er gitt ved

\mathbf {E} (\mathbf {r} )={q \over 4\pi \varepsilon _{0}r^{2}}{\hat {\mathbf {r} }}={q\,\mathbf {r}  \over 4\pi \varepsilon _{0}|\mathbf {r} |^{3}}

når den befinner seg i origo og ${\hat {\mathbf {r} }}$ = r/r er en enhetsvektor i radiell retning med r = |r|. Her er 1/4π ε₀ Coulombs konstant i SI-systemet som oftest brukes i dag. Feltvektorene peker derfor ut fra origo og med lengder som avtar med kvadratet av avstanden til ladningen. I stedet for å beskrive feltet med slike feltvektorer, er det mer vanlig å bruke feltlinjer. Det er kontinuerlige kurver som i hvert punkt har vektorfeltet som tangent.^[4]

Når man har mange ladninger q_i plassert i faste posisjoner r_i, blir det resulterende feltet i posisjon r gitt med vektorsummen av feltene fra hver av dem,

\mathbf {E} (\mathbf {r} )=\sum _{i}{q_{i}(\mathbf {r} -\mathbf {r} _{i}) \over 4\pi \varepsilon _{0}|\mathbf {r} -\mathbf {r} _{i}|^{3}}.

Det elektriske feltet oppfyller derfor superposisjonsprinsippet. Ofte kan det benyttes til å forenkle beregning av feltet.^[5]

I mange tilfeller kan ladningene som skaper elektriske felt, betraktes å være kontinuerlig fordelt. En slik fordeling i rommet vil ha en ladningstetthet ρ slik at ladningen i et lite volumelement rundt kildepunktet r ' kan skrives på den differensialle formen dq ' = ρ(r ')d³x '. Ved integrasjon over hele ladningsfordelingen finnes det totale feltet,

\mathbf {E} (\mathbf {r} )=\int d^{3}x'{\rho (\mathbf {r} ')(\mathbf {r} -\mathbf {r} ') \over 4\pi \varepsilon _{0}|\mathbf {r} -\mathbf {r} '|^{3}}.

På same måte kan man beregne feltet fra kontinuerlige fordelinger av elektrisk ladning på flater, langs kurver eller på linjer. Todimensjonal ladningsfordeling på en flate betegnes vanligvis med symbolet σ, mens langs en linje bruker man oftest λ.

Elektrisk fluks rediger

Desto tettere de elektriske feltlinjene er i et område av rommet, desto sterkere er feltet. Et kvalitativt mål for dette kan man få ved å beregne hvor mange feltlinjer som går gjennom en fiktiv flate S i denne delen av rommet. Denne størrelsen er gitt ved integralet

\Phi _{E}(S)=\int _{S}\mathbf {E} \cdot d\mathbf {S}

hvor d S = dS n er et lite flateelement som har enhetsvektoren n som normal. Verdien av integralet kalles den elektriske fluksen gjennom flaten og tilsvarer definisjonen av magnetisk fluks. Navnet kommer fra det analoge integralet i hydrodynamikk hvor det gir mengden av vann som strømmer gjennom en slik flate. Feltstyrken E kan derfor også kalles for «elektrisk flukstetthet».

I utgangspunktet sier Coulombs lov hva det elektriske feltet er utenfor en punktladning. En mer generell formulering er Gauss' lov som kan benyttes i mange andre sammenhenger. Den sier at den totale, elektriske fluksen gjennom enhver lukket flate er gitt ved den totale ladningen innenfor flaten. På integralform skrives den som

\Phi _{E}=\oint _{S}\mathbf {E} \cdot d\mathbf {S} ={Q \over \varepsilon _{0}}

Den tenkte flaten S kan legges hvor man måtte ønske og kalles en «Gauss-flate». Vanligvis velges den på en slik måte at integrasjonen blir enklest mulig. Det valget er i stor grad bestemt av symmetrien i problemet. Befinner det seg ingen ladninger innenfor flaten, sier loven derfor at like mye fluks må gå inn i flaten som det går ut av den.

Eksempel: Ladet kule rediger

Sfærisk ladningsfordeling med radius R samt to Gauss-flater med radius r innenfor og r' er utenfor.

For å beregne feltet inne i en kule med radius R og konstant ladningstetthet ρ, kan man legge en sfærisk Gauss-flate med radius r og med sentrum i kulens midtpunkt. På grunn av symmetrien må feltet være rettet i radiell retning. Fluksen gjennom Gauss-flaten er dermed E⋅4π r², mens den totale ladning innenfor flaten er (4/3)⋅ρπ r³. Gauss' lov gir da at feltet inni kulen er

E={\rho r \over 3\varepsilon _{0}}

Det er null i kulens sentrum r = 0 og har verdien ρR/3ε₀ på dens overflate r = R. Hvis Gauss-flaten har radius r' > R, omslutter den hele ladningen Q = (4/3)⋅ρπ R³ til kulen. I dette området utenfor kulen avtar feltet derfor som

E={Q \over 4\pi \varepsilon _{0}r^{2}}

i overensstemmelse med Coulombs lov. Setter man her r = R, finner man igjen verdien av feltet som resulterte fra beregningen inni kula. Det elektriske feltet er kontinuerlig på overflaten da det ikke finnes ladninger der.

At det elektriske feltet utenfor en sfærisk ladningsfordeling med totalladning Q er det samme som feltet fra en punktladning Q i kulens sentrum, er et eksempel på Newtons skallteorem. Grunnen er at Coulombs lov har samme matematiske form som Newtons gravitasjonslov. En annen konsekvens av dette teoremet er da at det elektriske feltet innenfor et kuleskall er null. Utenfor er feltet det samme som om kuleskallets totalladning var plassert i dets sentrum. Dette er også i overensstemmelse med Gauss' teorem.

Differensiell form av Gauss' lov rediger

Det lukkete flateintegralet som inngår på venstre side av Gauss' lov, kan omskrives ved bruk av divergensteoremet. Det sier at

\oint _{S}d\mathbf {S} \cdot \mathbf {E} (\mathbf {x} )=\int dV\,{\boldsymbol {\nabla }}\cdot \mathbf {E} (\mathbf {x} )

hvor V er volumet som flaten S omslutter. Men den totale ladningen Q som denne flaten omslutter, kan også skrives som et volumintegral over den elektriske ladningstettheten ρ(x),

Q=\int dV\,\rho (\mathbf {x} )

Begge sider av loven er dermed gitt ved integral over det samme volumet. Siden dette kan velges fritt, må de to integrandene være de samme. Det betyr at

{\boldsymbol {\nabla }}\cdot \mathbf {E} (\mathbf {x} )={1 \over \varepsilon _{0}}\rho (\mathbf {x} )

som må gjelde i hvert punkt i rommet. Dette er den «lokale» eller differensielle formen av Gauss' lov. Den sier at hver feltlinje starter på en positiv ladning og ender på en tilsvarende negativ ladning.^[4]

Når feltet er radielt rettet i tre dimensjoner, må divergensen regnes ut i kulekoordinater. Da kan divergensen skrives som

{\boldsymbol {\nabla }}\cdot \mathbf {E} ={1 \over r^{2}}{\partial  \over \partial r}(r^{2}E)={\partial E \over \partial r}+{2 \over r}E

For den ladete kulen med E = ρr/3ε₀, blir da ∇ ⋅ E = ρ/ε₀ som forventet. Samme formel gir også at denne divergensen er null utenfor kulen hvor feltet varierer som 1/r².

Punktladning rediger

En matematisk punktladning i punktet r' har en ladningstetthet som er uendelig stor i dette punktet og null utenfor slik at integralet over hele ladningsfordelingen gir en totalladning q. Dette tilsvarer definisjonen av Diracs deltafunksjon som tillater å skrive en slik ladningstetthet som

\rho (\mathbf {r} )=q\delta (\mathbf {r} -\mathbf {r'} )

Da det elektriske feltet fra denne ladningen er gitt ved Coulomb-feltet, gir Gauss' lov den matematiske sammenhengen

{\boldsymbol {\nabla }}\cdot {\mathbf {r} -\mathbf {r'}  \over |\mathbf {r} -\mathbf {r'} |^{3}}=4\pi \delta (\mathbf {r} -\mathbf {r'} )

Den opptrer i mange sammenhenger både i elektrostatikken og magnetostatikken.

Ladninger på linjer og plan rediger

I allminnelighet er det meget vanskelig å beregne det elektriske feltet nøyaktig for en generell ladningsfordeling. Men noen ganger lar det seg gjøre mer direkte. Det gjelder spesielt når problemet har en eller annen symmetri som forenkler oppgaven. For eksempel, for en sfærisk symmetrisk ladningsfordeling vil alle retninger være av samme betydning. Derav kan man med en gang si at det elektriske feltet må være radielt og ha samme størrelse i punkt med samme avstand fra fordelingens sentrum. Dette gjelder opplagt for en punktladning, men det gjelder like godt for en kuleformet, utstrakt fordeling hvor ladningen er uniformt fordelt.

Linjeladning rediger

Feltet fra to motsatt plasserte linjeelement langs y-aksen gir et resulterende felt langs x-aksen.

Feltet fra uendelig lang, rett linje med en konstant, lineær ladningstetthet λ, kan ikke variere med posisjonen langs linjen da alt må forbli uforandret ved en slik forflytning. Det kan derfor bare variere med avstanden fra linjen.

Plasseres linjeladningen langs y-aksen, vil et lite intervall dy på denne i avstand +y fra origo ha ladningen λdy. Feltet fra dette intervallet har da størrelsen λdy/4πε₀R² hvor R angir avstanden til feltpunktet. Har dette avstanden x fra y-aksen, er denne gitte ved Pytagoras’ læresetning som R² = x² + y². Da det også vil være et tilsvarende bidrag fra et tilsvarende intervall i punktet -y, vil summen av disse to gi en feltvektor normalt på y-aksen. Denne komponenten finnes ved å multiplisere hvert av disse bidragene med x/R. Det totale feltet i avstanden x fra linjen finnes nå ved å integrere opp alle disse bidragene fra hele linjen,

E={\lambda  \over 4\pi \varepsilon _{0}}\int _{-\infty }^{\infty }{xdy \over (x^{2}+y^{2})^{3/2}}={\lambda  \over 2\pi \varepsilon _{0}x}

En mer direkte vei å finne dette resultatet følger fra Gauss' lov ved å omslutte linjeladningen med en sylinderformet Gauss-flate. Ut fra symmetri er de elektriske feltvektorene rettet radielt utover og står derfor normalt på sylinderflaten. Har denne sylinderen radius r og høyde h, vil fluksen gjennom den være 2πrhE. Da flaten omslutter en total ladning λh, får man med en gang at E = λ/2πε₀r hvor r igjen er avstanden til linjeladningen.

Dette resulatet er også omtrentlig riktig for en endelig lang linjeladning så lenge som man betrakter felt i nærheten av midten til linjen. Ved dens endepunkt er feltet ikke rettet radielt utover.^[6]

Ladet plan rediger

For et plan med konstant flateladning σ vil de elektiske feltvektorene stå normalt på planet, igjen ut fra symmetri. Hvis det ligger i xy-planet, kan man betrakte denne todimensjonale ladningsfordelingen som bestående av en uendelig rekke med parallelle linjeladninger som er parallelle med y-aksen, hver med en linjeladning λ = σdx. Feltet fra en slik linje i avstand x fra y-aksen er fra det foregående gitt som σdx/2πε₀R hvor nå R angir avstanden fra denne linjen til feltpunktet i avstand z over origo, det vil si R² = x² + z². Men da det bare er komponentene normalt på planet som bidrar, må dette bidraget multipliseres med z/R. Det totale feltet i avstand z fra planet er derfor

E={\sigma  \over 2\pi \varepsilon _{0}}\int _{-\infty }^{\infty }{zdx \over x^{2}+z^{2}}={\sigma  \over 2\varepsilon _{0}}

At resultatet er det samme uavhengig av avstanden til planet, har mange viktige konsekvenser. Det følger også fra Gauss' lov ved å legge igjen en sylinderformet flate som står normalt på det og omslutter en liten del med areal A. Dette er også arealet til toppen og bunnen av sylinderen hvor fluksen går ut på begge sider av planet. I alt forlater derfor en fluks 2EA sylinderen som skyldes ladningen σA innenfor. Dermed finner man igjen at E = σ/2ε₀.

Ladet ring rediger

Det elektriske feltet i et punkt P på ringens akse fra linjeelementet ds.

En annen, symmetrisk linjeladning er en ring med radius a og konstant ladningstetthet λ. Den totale ladningen på ringen er derfor q = 2πaλ. Med en gang kan man da si at feltet er null ringens sentrum. Det skyldes at feltet fra ladningen i et punkt på ringen blir nøyaktig opphevet av feltet fra det diametralt motsatte punktet.

På samme måte har punktene langs en linje normalt på ringen og gjennom dens sentrum en spesielt symmetrisk plassering. Dette er ringens akse. Der vil bidragene fra to diametralt plasserte punkt på ringen gi et resulterende felt som peker langs z-aksen hvis ringen ligger i xy-planet. Et lite stykke av ringen med lengde ds vil gi et felt med størrelse λds/4πε₀R² hvor R angir avstanden fra denne ladningen til feltpunktet P i avstand z over ringen. Her er nå R² = a² + z². Når vi summerer opp alle disse bidragene fra punkter langs ringen, er det bare brøkdelen z/R av dette feltet langs ringens akse som vil bidra. I andre retninger vil komponentene kansellere ut. Da integralet av ds er omkretsen 2π a, blir dermed feltet langs z-aksen

E={qz \over 4\pi \varepsilon _{0}(a^{2}+z^{2})^{3/2}}

I ringens sentrum er z = 0. Feltet er der null som forventet. Langt fra ringen hvor z >> a, er reduseres dette resultatet til E = q/4πε₀z². I sin slik posisjon ser ringen ut som en enkel punktladning i avstand z og feltet er ganske enkelt gitt ved Coulombs lov.^[1]

Ladet disk rediger

Dette resultatet for en ladet ring, gjør det mulig også finne feltet på aksen til en ladet disk med konstant flateladningstetthet σ. Man betrakter da den som satt sammen av konsentriske ringer med variabel radius r. En slik ring med tykkelse dr har ladningen dq = 2πrdr. Har disken radius R, finner man ved integrasjon over alle ringene at feltet på aksen i avstand z blir

E={\sigma z \over 4\pi \varepsilon _{0}}\int _{-\infty }^{\infty }{2\pi rdr \over (r^{2}+z^{2})^{3/2}}={\sigma  \over 2\varepsilon _{0}}\left(1-{z \over {\sqrt {z^{2}+R^{2}}}}\right)

I grensen R → ∞ går disken over til å bli et uendelig plan hvor feltstyrken utenfor igjen sees å anta den konstante verdien E = σ/2ε₀.

Ledere og dielektrika rediger

Feltet utenfor en uniformt ladet plate er det samme uansett hva den er laget av. I et dielektrisk materiale som er en isolator kan ikke ladninger bevege seg fritt omkring, men kan plasseres i faste posisjoner. Har platen et areal A, vil en total ladning Q da kunne plasseres uniform inne i den slik at den har flatetettheten σ = Q/A . Feltet på hver side av platen har da den konstante verdien E = σ/2ε₀ = Q/2Aε₀. Derimot varierer feltet inni platen med verdien E = 0 i midten og er lineært voksende ut til overflaten hvor det tar den konstante verdien.

Er platen derimot en elektrisk leder, vil ladningen Q fordele seg på overflaten av lederen slik at feltet inne i platen blir nøyaktig lik null. Hver av overflatene har da ladningstettheten σ' = Q/2A og skaper feltene E' = σ' /2ε₀ som peker ut fra lederen og inn i metallet. I metallet virker disse to delfeltene i motsatt retning slik at der blir totaltfeltet E = 0 som det skal være. Men utenfor lederen adderer de seg opp slik at der blir feltet E = 2E' = σ' /ε₀ = Q/2Aε₀.

Dette resultatet kan også forstås med en sylindrisk Gauss-flate med topp og bunn parallelle til metalloverflaten med bunnen innfor og toppen utenfor. Da går det fluks bare ut gjennom toppflaten da feltet gjennom bunnen inni i lederen er null. I elektrostatikken er denne egenskapen til det elektriske feltet nær ledere av stor betydning. Denne oppførselen av det elektriske feltet forklarer også virkningen til et Faraday-bur.^[1]

Elektrisk potensial rediger

Det elektriske feltet kan utledes fra et elektrisk potensial. Ofte blir det betegnet som U, men det er også vanlig å angi det som V. I mer teoretiske arbeid blir også Φ benyttet.

En enkel måte å vise hvordan det oppstår, er å gjøre bruk av resultatet

{\boldsymbol {\nabla }}{1 \over |\mathbf {r} -\mathbf {r} '|}=-{\mathbf {r} -\mathbf {r} ' \over |\mathbf {r} -\mathbf {r} '|^{3}}

som kommer frem ved direkte derivasjon.^[5] Feltet fra en kontinuerlig ladningsfordeling i rommet kan derfor skrives som E = - ∇V hvor det elektriske potensialet er

V(\mathbf {r} )=\int d^{3}x'{\rho (\mathbf {r} ') \over 4\pi \varepsilon _{0}|\mathbf {r} -\mathbf {r} '|}.

En elektrisk ladning q i dette potensialet vil ha den potensielle energien U(r) = qV(r). Denne varierer med posisjonen, noe som betyr at ladningen er utsatt for en kraft F = -∇ U. Dette er akkurat kraften F = q E fra det elektriske feltet.

Ved mange beregninger av elektriske felt er det ofte enklere å først regne ut potensialet som er en skalar størrelse. At feltet er gitt som gradienten av potensialet, betyr at det er konservativt og oppfyller ∇ × E = 0. Dette er Maxwells tredje ligning for det elektrostatiske feltet.

Gauss' lov ∇ ⋅ E = ρ/ε₀ uttrykt ved potensialet gir

\nabla ^{2}V(\mathbf {x} )=-{1 \over \varepsilon _{0}}\rho (\mathbf {x} )

som er Poissons ligning. Den er en andreordens, partiell differensialligning. For en gitt ladningsfordeling kan den i prinsippet løses og gi potensialet overalt. Der det ikke finnes ladninger, er ρ = 0 og ligningen reduseres til Laplace-ligningen. Kjenner man potensialet overalt, kan det elektriske feltet beregnes ved en enkel derivasjon. Dette er ofte mye enklere enn å beregne feltet direkte fra ladningene da potensialet er en skalar størrelse.^[6]

Kondensator rediger

Elektriske feltlinjer i en oppladet plate-kondensator.

En elektrisk kondensator kan lagre elektrisk ladning og er en videreføring av den opprinnelige Leidnerflasken. Den enkleste utgaven er en «platekondensator» som består av to parallelle, ledende plater som holdes i en viss avstand d fra hverandre. Fra en ytre spenningskilde kan disse lades opp slik at de bærer motsatte ladninger ±Q. Hvis hver plate antas å ha arealet A og deres avstand d er tilstrekkelig liten, er det elektriske feltet fra hver av dem det samme som om de var uendelig store. Feltvektorene vil da overalt stå normalt på platene og ha størrelse Q/2Aε₀ fra hver av dem når man antar at det er luft eller vakum mellom platene. Hvis det er et annet, isolerende materiale mellom platene enn luft, må ε₀ erstattes med materialets dielektrisitetskonstant ε.^[4]

Utenfor platene ville de to feltene kansellere hverandre, mens mellom platene peker de i samme retning og gir totalfeltet E = Q/Aε₀. Dette er konstant slik at den elektriske spenningen eller potensialet mellom platene er V = Ed. Ladningen på platene kan da uttrykkes ved spenningen som Q = CV hvor

C=\varepsilon _{0}{A \over d}

er konsensatorens kapasitans. Den sier hvor mye ladning den kan lagre under en gitt spenning.

Elektrisk feltenergi rediger

Mellom de to platene virker det en kraft som trekker dem mot hverandre og som vanligvis blir nøytralisert på mekanisk vis. Denne elektriske kraften er et uttrykk for at kondensatoren inneholder en elektrisk energi som ligger lagret i feltet mellom platene. Denne energien er tilført via arbeidet som må utføres for å lade kondensatoren opp. Man tenker seg at man starter med en uladet kondensator med null spenning. Så gjennomfører man en serie med flytninger av små ladninger dq fra den ene platene til den andre til man til slutt har ladningene ±Q på hver av dem. Før denne tilstanden er nådd, vil de ha ladningene ±q med spenningen V = q/C. Flytter man så en ny ladning dq, utføres et lite arbeid slik at energien til kondensatoren øker med dU = V dq. Totalenergien ved full oppladning blir dermed

U_{E}={1 \over C}\int _{0}^{Q}qdq={Q^{2} \over 2C}={1 \over 2}QV={1 \over 2}CV^{2}

Uttrykt ved feltet kan dette skrives som

U_{E}={1 \over 2}\varepsilon _{0}AdE^{2}

Men her er Ad volumet av rommet mellom platene, det vil si volumet til det elektriske feltet. Det kan derfor tilskrives en «elektrisk feltenergitetthet» U/Ad som er

u_{E}={1 \over 2}\varepsilon _{0}E^{2}

Her er denne konstant mellom platene. Men en mer generell utledning i elektrostatikken viser at dette er det generelle uttrykket for den elektriske energitettheten også for et felt som varierer i tid og rom. Et tilsvarende resultat gjelder for energitettheten i det magnetiske feltet.^[7]

Dipolfeltet rediger

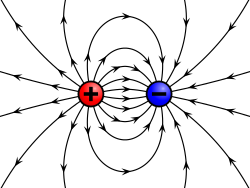
Illustrasjon av det elektriske feltet rundt en positiv (rød) og en negativ (grønn) ladning.

Det elektrisk feltet fra en positiv og en like stor, men negativ ladning, kalles et «dipolfelt» i grensen hvor avstanden mellom dem blir tilstrekkelig liten. Betrakter man en Gauss-flate som omslutter begge ladningene, er da totalladningen innenfor flaten null. Like mye fluks må derfor gå ut av flaten som går inn i den. Derfor vil det elektriske feltet i stor avstand fra ladningene avta raskere enn 1/r².

For å beregne feltet fra dipolen antar man at de er skapt av to punktladninger q og -q som er separert med avstandsvektoren d som går fra den negative til den positive ladningen. Plasseres disse symmetrisk om origo, vil feltet i et punkt r består da av Coulomb-feltet fra den positive ladningen på stedet d/2 pluss feltet fra den negative ladningen i posisjon -d/2, det vil si

\mathbf {E} (\mathbf {r} )={q \over 4\pi \varepsilon _{0}}\left({\mathbf {r} -\mathbf {d} /2 \over |\mathbf {r} -\mathbf {d} /2|^{3}}-{\mathbf {r} +\mathbf {d} /2 \over |\mathbf {r} +\mathbf {d} /2|^{3}}\right)

I dipolgrensen hvor avstanden mellom ladningene d = |d| << |r| = r, kan man skrive

|\mathbf {r} \pm \mathbf {d} /2|^{3}=r^{2}\pm \mathbf {r} \cdot \mathbf {d} +d^{2}/4)^{3/2}=r(r^{2}\pm {3 \over 2}\mathbf {r} \cdot \mathbf {d} )

når man ser bort fra høyere ordens ledd. Innsatt gir dette totalfeltet fra dipolen

\mathbf {E} (\mathbf {r} )={1 \over 4\pi \varepsilon _{0}r^{3}}{\Big [}3(\mathbf {p} \cdot {\hat {\mathbf {r} }}){\hat {\mathbf {r} }}-\mathbf {p} {\Big ]}

uttrykt ved enhetsvektoren ${\hat {\mathbf {r} }}$ = r/r og det elektriske dipolmomentet p = q d for de to ladningene. Det er en vektor med retning fra den negative til den positive ladningen. Dipolfeltet er symmetrisk om denne retningen.

Som et eksempel på bruk av dette resultatet, kan man betrakte en dipol i origo som ligger langs den positive x-aksen. Da blir feltet lenger ut til høyre på denne aksen E = 2p e_x/4πε₀x³, mens det i et punkt på y-aksen er E = -p e_x/4πε₀y³.

I stedet for å beregne komponentene til dipolfeltet i kartesiske koordinater, kan man benytte polarkoordinater (r,θ). Feltvektoren har da de to komponentene^[5]

E_{r}={2p \over 4\pi \varepsilon _{0}r^{3}}\cos \theta ,\;\;\;E_{\theta }={p \over 4\pi \varepsilon _{0}r^{3}}\sin \theta

For punkter på x-aksen, henholdsvis y-aksen, er disse i overensstemmelse med resultatet for de kartesiske komponentene.

Dipolpotensialet rediger

Feltlinjer fra en positiv og en negativ ladning som tilsammen utgjør en elektrisk dipol.

Det elektriske potensialet til en dipol følger direkte fra det mindre kompliserte uttrykket

V(\mathbf {r} )={q \over 4\pi \varepsilon _{0}}\left({1 \over |\mathbf {r} -\mathbf {d} /2|}-{1 \over |\mathbf {r} +\mathbf {d} /2|}\right)

For store avstander kan dette forenkles på samme måte som for beregning av feltet. Resultatet kan skrives på den kompakte formen

V(\mathbf {r} )={\mathbf {p} \cdot \mathbf {r}  \over 4\pi \varepsilon _{0}r^{3}}

Dipolfeltet kan nå gjenfinnes fra E = - ∇V . Det står overalt vinkelrett på flater gitt ved en konstant verdi av potensialet, det vil si det som kalles ekvipotensialflater.

Ved bruk av polarkoordinater tar dipolpotensialet formen

V(\mathbf {r} )={p\cos \theta  \over 4\pi \varepsilon _{0}r^{2}}

når dipolen ligger langs den positive x-aksen slik at p⋅r = pr cosθ. De to komponentene finnes nå lett fra gradienten i dette koordinatsystemet som gir E_r = - ∂V/∂r og E_θ = - (1/r)∂V/∂θ. Det gir det samme resultatet for disse komponentene på en mer direkte måte.

Multipoler rediger

Et dipolpotensial kan oppstå fra ladningsfordelinger med mer enn to partikler. Har man like mange positive som negative ladninger q_i i posisjoner r_i, defineres deres dipolmoment som

\mathbf {p} =\sum _{i}q_{i}\mathbf {r} _{i}

Tar man med høyere ordens ledd i utviklingen av potensialet fra hver av ladningene, vil det resulterende potensialet inneholde ledd som avtar med avstanden raskere enn dipolpotensialet. Dette kalles en multipolutvikling. For eksempel kan to positive og to negative ladninger som alle ligger nær hverandre, betraktes som to dipoler som ligger nær hverandre. Avhengig av deres relative plassering, kan de da gi opphav til et «kvadrupolpotensial». Dette kan regnes ut fra dipolpotensialet på samme måte som at dette kan regnes ut fra Coulomb-potensialet for to motsatte ladninger som ligger nær hverandre.

Dipol i ytre felt rediger

Elektrisk dipol p danner vinkel θ med ytre felt E.

Dipolpotensialet må ikke forveksles med den potensielle energien for en dipol i et ytre, elektriske felt. Et slikt felt virker på hver av ladningene som utgjør dipolen. Resultatet er at kreftene som dette ytre feltet forårsaker, vil dreie dipolen slik at den peker mest mulig langs feltet. Den har da minimal, potensiell energi.

En dipole består av en ladning q₁ = q i posisjon r₁ og en ladning q₂ = -q i posisjon r₂ med gjensidig avstand d = r₁ - r₂. Befinner den seg i et ytre, elektrisk felt E(r), er den totale kraften som virker på den

\mathbf {F} =q_{1}\mathbf {E} (\mathbf {r} _{1})+q_{2}\mathbf {E} (\mathbf {r} _{2})=q(\mathbf {E} (\mathbf {r} _{1})-\mathbf {E} (\mathbf {r} _{2}))

Er feltet det samme overalt, vil differansen i parentesen være null og totalkraften er null. Kraften som virker på den ene ladningen blir opphevet av kraften på den andre ladningen. Tyngdepunktet til dipolen vil derfor ikke flytte seg i dette feltet.

Men disse to, motsatte rettete kreftene F₁ og F₂ utgjør et dreiemoment. Når dette beregnes om dipolens tyngdepunkt, har det størrelsen

{\begin{aligned}\mathbf {T} &={1 \over 2}\mathbf {d} \times \mathbf {F} _{1}-{1 \over 2}\mathbf {d} \times \mathbf {F} _{2}={1 \over 2}\mathbf {d} \times q\mathbf {E} +{1 \over 2}\mathbf {d} \times q\mathbf {E} \\&=\mathbf {p} \times \mathbf {E} \end{aligned}}

hvor dipolmomentet er p = q d. Størrelsen til dreiemomentet kan skrives som pE sinθ når man innfører vinkelen θ mellom feltvektoren og dipolens retning. Det er derfor forskjellig fra null bortsett fra når dipolen har samme retning som det ytre feltet.

Potensiell energi rediger

Dreiemomentet er et uttrykk for at dipolen kan utføre et arbeid ved rotasjon i feltet. Den har derfor en potensiell energi som kan relateres til potensialet V for det ytre feltet E = - ∇ V ut fra definisjonen som

{\begin{aligned}U&=q_{1}V(\mathbf {r} _{1})+q_{2}V(\mathbf {r} _{2})=q(V(\mathbf {r} _{1})-V(\mathbf {r} _{2}))=-q\int _{2}^{1}d\mathbf {r} \cdot \mathbf {E} =-q(\mathbf {r} _{1}-\mathbf {r} _{2})\cdot \mathbf {E} \\&=-q\,\mathbf {d} \cdot \mathbf {E} =-\mathbf {p} \cdot \mathbf {E} \end{aligned}}

Da størrelsen til denne energien er -pE cosθ, vil dipolen ha minst energi -pE når den peker langs det elektriske feltet slik at vinkelen θ = 0. Peker den i motsatt retning, vil derimot energien være maksimal med størrelse pE . Selv om dreiemomentet som da virker på den er null, vil den minste forstyrrelse fra denne retningen forårsake at dipolen prøver å rotere inn i likevektsstillingen med lavest energi. Disse to størrelsene er forbundet ved relasjonen T = - ∂U/∂θ som er typisk for sammenhengen mellom arbeid og energi.

Inhomogent felt rediger

Når en dipole befinner seg i et felt som ikke er konstant, vil kreftene på de to ladningene ikke lenger oppheve hverandre. I stedet virker det en resulterende kraft på den som er

{\begin{aligned}\mathbf {F} &=q\mathbf {E} (\mathbf {r} +\mathbf {d} /2)-q\mathbf {E} (\mathbf {r} -\mathbf {d} /2)=q\mathbf {E} +q(\mathbf {d} /2\cdot {\boldsymbol {\nabla }})\mathbf {E} -q\mathbf {E} +q(\mathbf {d} /2\cdot {\boldsymbol {\nabla }})\mathbf {E} \\&=(\mathbf {p} \cdot {\boldsymbol {\nabla }})\mathbf {E} =p_{x}{\partial \mathbf {E}  \over \partial x}+p_{y}{\partial \mathbf {E}  \over \partial y}+p_{z}{\partial \mathbf {E}  \over \partial z}\end{aligned}}

Det ytre feltet vil nå påvirke dipolen med et dreiemoment som vil forsøke å rotere den samt en ekstra kraft som vil forsøke å flytte den i rommet. Retningen til denne forflytningen er i alminnelighet ikke i samme retning som det ytre feltet.

Egenskaper til magnetiske dipoler i et ytre, magnetisk felt er beskrevet ved helt tilsvarende ligninger som for elektriske dipoler her. Grunnen er at en magnetisk dipol kan tenkes oppbygd av to motsatt ladete, magnetiske monopoler. Selv om disse monopolene ikke finnes, gir et slikt bilde likevel en riktig beskrivelse. Det sies å være en brukbar «modell» for en magnetisk dipol.^[4]

Elektrisk polarisasjon rediger

Polarisasjon av det dielektriske materialet i en platekondensator.

Et dielektrisk materiale er en elektrisk isolator som består av atomer eller molekyler som kan «polariseres» under påvirkning av et elektrisk felt. Det betyr at de har et elektrisk dipolmoment som vil forsøke å rette seg inn langs det ytre feltet. Brukes et slikt materiale i en kondensator i stedet for luft, vil det elektriske feltet mellom de metalliske platene reduseres. For eksempel, tett opp til den positive platen vil de negative endene til de nærmeste dipolene i materialet tiltrekkes mot platen og effektivt redusere ladningen på denne selv om dipolladningene fremdeles sitter fast i materialet. Og tilsvarende vil den negative platen få sin ladningstetthet effektivt redusert.

Før det dielektriske materialet blir satt inn mellom platene, har hver ladningstettheten σ = Q/A slik at feltet mellom dem er σ/ε₀. Etter at materialet er innsatt, er den effektive ladningstettheten ved hver plate redusert som igjen resulterer i et mindre, elektrisk felt E = (σ - σ_b)/ε₀ der reduksjonen skyldes dipolladningene som har vendt seg langs det påtrykte feltet. Denne induserte ladningstettheten kan uttrykkes ved polarisasjonen P til materialet som σ_b = P. Dimensjonen til denne nye størrelsen er derfor C/m² og lik med dimensjonen til flateladningstettheten.

Det er vanlig å definere det elektriske feltet i et materiale som skyldes de frie ladningene ±Q på platene som forskyvningsfeltet D = σ. Dette er tilstede sammen med det vanlige, elektriske feltet E inni materialet. Sammenhengen mellom disse to i en platekondensator sees nå å være D = ε₀E + P. Men disse tre størrelsene kan ikke være uavhengige av hverandre da polarisasjonen i allminnelighet avhenger av det elektriske feltet.^[7]

Lineært materiale rediger

Vanligvis øker polarisasjonen proporsjonalt med det elektriske feltet. Man har da den lineære sammenhengen P = ε₀χ_eE hvor proporsjonalitetskonstanten χ_e kalles den elektriske susceptibiliteten til materialet og er et dimensjonsløst tall som kan forventes å være postivt. Da kan det elektriske feltet i platekondensatoren skrives som E = E₀/(1 + χ_e) uttrykt ved feltet E₀ = σ/ε₀ mellom flatene før materialet ble innsatt. Det er derfor blitt redusert med faktoren ε_r = 1 + χ_e som er den relative permittivitet til materialet. Da σ = Q/A , betyr det at kapasiteten til platekondensateren dermed er øket til

C=\varepsilon _{0}(1+\chi _{e}){A \over d}

når avstanden mellom platene er d. En kondensator med et dielektrikum kan derfor lagre en mye større ladning for en gitt spenning.

Det elektriske feltet er en vektoriell størrelse. Derfor vil den elektriske polarisasjonen også være beskrevet ved et vektorfelt som i et lineært og homogent medium kan skrives som P = ε₀χ_e E. På overflaten av materialet vil det da formes en indusert ladningstetthet

\sigma _{b}=\mathbf {P} \cdot {\hat {\mathbf {n} }}

hvor enhetsvektoren ${\hat {\mathbf {n} }}$ står normalt på flaten. Men hvis polarisasjonen ikke er konstant, vil den også indusere en romlig ladningstetthet

\rho _{b}=-{\boldsymbol {\nabla }}\cdot \mathbf {P}

som består av bundne dipolladninger inni materialet som er forskjøvet litt i forhold til hverandre.

Forskyvningsfeltet vil også være en vektor som nå blir

\mathbf {D} =\varepsilon _{0}\mathbf {E} +\mathbf {P}

Da det elektriske feltet i hvert punkt i materialet skyldes et samspill av all ladninger, fri og bundne, må det alltid oppfylle Gauss' lov. Lokalt i materialet tar den da formen ∇⋅E = (ρ + ρ_b)/ε₀. Det betyr at forskyvningsfeltet oppfyller Gauss' lov på den mer generelle formen

{\boldsymbol {\nabla }}\cdot \mathbf {D} =\rho

hvor forskyvningsfeltet nå kan skrives som D = ε E med permittiviteten ε = ε₀(1 + χ_e). Dette feltet kan derfor tilskrives fri ladninger alene. Dette er Maxwells første ligning på sin mest generelle form.

Elektrodynamikk rediger

Elektriske ladninger som beveger seg, skaper et magnetisk felt som kan beregnes fra Biot-Savarts lov. Dette vil opptre sammen med det elektriske feltet fra ladningene. Den elektrostatiske beskrivelsen må da erstattes av en mer generell elektrodynamikk som omhandler både elektriske og magnetiske felt skapt av ladninger i bevegelse. Disse feltene vil i allminnelighet variere med tiden og må beskrives ved å ta alle Maxwells ligninger i bruk.^[6]

På samme måte som det elektriske feltet i det statiske tilfellet er gitt som gradienten av et skalart potensial V, er det magnetisk feltet alltid gitt som curl av et vektorpotensial A,

\mathbf {B} ={\boldsymbol {\nabla }}\times \mathbf {A}

Dette gjelder også når feltene varierer med tiden. Faradays induksjonslov ∇ × E = - ∂B/∂t kan da skrives som

{\boldsymbol {\nabla }}\times {\Big (}\mathbf {E} +{\partial \mathbf {A}  \over \partial t}{\Big )}=0

Innholdet i parentesen må derfor være en gradient for at curl av innholdet alltid skal gi null. Og den gradienten må stemme overens med uttrykket for det elektriske feltet i det statiske tilfellet. Derfor er dette feltet generelt gitt ved de to potensialene som

\mathbf {E} =-{\boldsymbol {\nabla }}V-{\partial \mathbf {A}  \over \partial t}

Dette siste leddet er i mange sammenhenger helt avgjørende for beskrivelsen av elektromagnetiske fenomen. Det følger også direkte fra den spesielle relativitetsteorien.^[8]

Kvanteelektrodynamikk rediger

I elektrodynamikk beskrives det elektriske feltet ved Maxwells ligninger, mens de ladete partiklene beskrives ved relativistisk mekanikk. Når denne klassiske beskrivelsen utvides ved bruk av kvantemekanikk, fremkommer kvanteelektrodynamikk. Det elektromagnetiske feltet må da forstås som et kvantefelt hvor kvantene er fotoner som kan absorberes og emitteres som partikler. Coulomb-kraften fremkommer ved utveksling av «virtuelle» fotoner mellom partikler som har elektrisk ladning. Disse er vanligvis elektroner som også må beskrives ved bruk av kvantefeltteori. Det tilsvarende feltet for elektronene er styrt av Dirac-ligningen som automatisk forklarer eksistensen av deres antipartikler som er positroner.

Det klassiske, tomme rommet eller vakuum vil i kvantelektrodynamikken bestå av en kokende suppe av virtuelle fotoner og virtuelle elektron-positron par. Avstanden mellom de to partiklene i et slikt par er gitt ved Compton-bølgelengden λ_e = ħ/m_ec . Hvis det er et elektrisk felt E i dette rommet, vil elektron-positron paret ha en elektrisk, potensiell energi eEλ_e. Er denne større enn hvileenergien 2m_ec² til de to virtuelle partiklene, vil de opptre som reelle og dermed frigjøres i feltet. Dette forklarer eksistensen av det kritiske, elektriske feltet E_c som ikke kan overstiges fordi vakuumet da brytes ned i pardannelse av elektroner og positroner.^[2]

Se også rediger

Referanser rediger

^ ^a ^b ^c H.D. Young og R.A. Freedman, University Physics, Addison-Wesley, New York (2008). ISBN 978-0-321-50130-1.
^ ^a ^b C. Itzykson and J-B. Zuber, Quantum Field Theory, McGraw-Hill, New York (1980). ISBN 0-07-032071-3.
^ A. Hansen and F. Ravndal, Klein’s Paradox and its Resolution, Physica Scripta 23, 1030–1042 (1981).
^ ^a ^b ^c ^d D. Halliday and R. Resnick, Fundamentals of Physics, John Wiley & Sons, New York (1988). ISBN 0-471-63736-X.
^ ^a ^b ^c D.J. Griffiths, Introduction to Electrodynamics, Prentice Hall, New Jersey (1999). ISBN 0-13-805326-X.
^ ^a ^b ^c J.R. Reitz and F.J. Milford, Foundations of Electromagnetic Theory, Addison-Wesley Publishing Company, Reading (1960).
^ ^a ^b O. Hunderi, J.R. Lien og G. Løvhøiden, Generell fysikk for universiteter og høgskoler, Bind 2, Universitetsforlaget, Oslo (2001). ISBN 978-82-1500-006-0.
^ R.P. Feynman, The Feynman Lectures on Physics, Vol II, Addison-Wesley, Longman. (1970). ISBN 978-0-201-02115-8.

Eksterne lenker rediger

Johannes Skaar, NTNU, Forelesninger TFE4120: Elektromagnetisme, Youtube (2017).
Walter Levin, MIT, Lectures on Electricity and Magnetism, Youtube (2015).
Hyperphysics, Electric Field of Line Charge.

[YF-1] H.D. Young og R.A. Freedman, University Physics, Addison-Wesley, New York (2008). ISBN 978-0-321-50130-1.

[IZ-2] C. Itzykson and J-B. Zuber, Quantum Field Theory, McGraw-Hill, New York (1980). ISBN 0-07-032071-3.

[3] A. Hansen and F. Ravndal, Klein’s Paradox and its Resolution, Physica Scripta 23, 1030–1042 (1981).

[HR-4] D. Halliday and R. Resnick, Fundamentals of Physics, John Wiley & Sons, New York (1988). ISBN 0-471-63736-X.

[Griffiths-5] D.J. Griffiths, Introduction to Electrodynamics, Prentice Hall, New Jersey (1999). ISBN 0-13-805326-X.

[RM-6] J.R. Reitz and F.J. Milford, Foundations of Electromagnetic Theory, Addison-Wesley Publishing Company, Reading (1960).

[HLL-7] O. Hunderi, J.R. Lien og G. Løvhøiden, Generell fysikk for universiteter og høgskoler, Bind 2, Universitetsforlaget, Oslo (2001). ISBN 978-82-1500-006-0.

[RPF-8] R.P. Feynman, The Feynman Lectures on Physics, Vol II, Addison-Wesley, Longman. (1970). ISBN 978-0-201-02115-8.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]